| Binary - Negative Numbers |
| Written by Mike James | ||||
| Sunday, 25 June 2023 | ||||
Page 2 of 3
Getting negativeAchieving addition so easily by the fusion of Boolean logic and binary doesn't really prepare you for the messiness of the next step - subtraction. So how do we implement subtraction? The first question is how do we represent a negative number? Notice that this is a very subtle question because subtraction is an operation whereas a negative number is a quantity. That is 6-5 is an instruction to subtract (take away) 5 things from 6 things but -3 is an absence of three things. You should also be able to see that negative numbers arise quite naturally from the operation of subtraction. What do you get if you subtract 6 apples from 5 apples? Answer minus one apples. Subtraction is such a horrible operation (if you are interested, its biggest failure is that it isn't commutative i.e. x-y isn't the same as y-x) it is much better to ignore it in favour of negative numbers. Any subtraction that you want to do can be achieved by adding a negative - which in turn raises the earlier question of how do we do we represent negative numbers? The twin problems of how do we do subtraction and how do we represent negative numbers, have a very neat single solution that was invented back in the days of mechanical decimal calculators. Mechanical calculators represent numbers using positions on a rotating disk or drum. They work much like a odometer in that ten turns of the units wheel, notches up one turn of the tens wheel and so on. To add one to a number you turn the units wheel on by one. Equally obviously you can subtract one by turning the units wheel the other way. Now consider what happens when the wheels are set up to read zero and you turn the units wheel back by one. If you are working with four-digit wheels then 0,0,0,0 becomes 9,9,9,9. There's nothing remarkable about this until you notice that subtracting one from zero gives you minus one and so in this system 9,9,9,9 must in some sense be a representation of minus one.
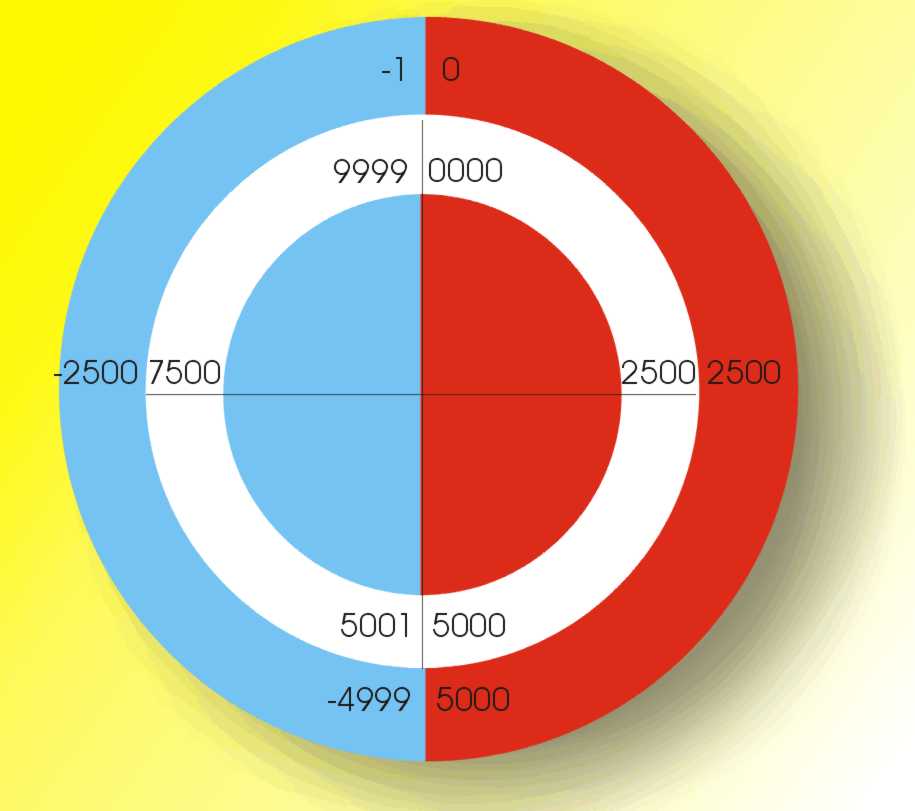
By the same reasoning 9,9,9,8 must be minus two, 9,9,9,7 minus three and so on. In general you can see that for a four-digit machine 10000-x is a representation of -x. Notice that you subtract x from a number with one more digit than the precision you are working at, i.e. 10000 has five digits. This observation that 10000-x is a representation of -x is more than just a surface detail. These representations even behave like negative numbers. For example, have a go at working out what you get if you add 9999 to 0100. The obvious answer is 10099 and this is just what you get when you add standard positive numbers together - but wait a minute; our supposed mechanical calculator only has four wheels how can it show 10099 which has five digits? The answer is that it can’t and what it actually shows as the answer is just 0099. So in four-wheel arithmetic the sum 0100+9999 gives the answer 0099 and you can see that as long as you ignore the “roll over” 9999 really does behave like minus one. In the same way 10000-x really does behave like -x when you add it to another number - as long as you remember to truncate to the number of digits we are working with. Thus we have our solution! Complementary arithmeticInstead of building a half and full subtractor circuit, something that could be done using the same methods developed for addition, all we have to do is use the trick of "add 10000-x" when we want to subtract x. Of course so far we have worked in decimal and assumed only four-digit arithmetic but it can all be generalised. In decimal the method is know as “ten's complement” arithmetic because to obtain the representation of -x you subtract it from 10^digits, i.e. ten raised to the power of the number of digits you are working with. In binary the same representation is called “two's complement” and the only difference is that you subtract x from 2^bits, where bits is the number of bits you are working with. It is important to remember that any extra bits you may obtain when you add numbers together have to be thrown away, i.e. you can’t extend your working range during arithmetic. What this means is that before you start doing arithmetic with negative number you have to fix the number of digits or bits that you regard as valid - and remember to throw any excess away. If you don't do this you will get the wrong answers. This may seem a bit crazy when you are doing pencil and paper arithmetic but it fits in perfectly with the way computers do arithmetic. That is, you might be able to write down another digit or bit but a 16-bit computer does 16-bit arithmetic no matter what! Two's complement sounds good but there are some complications. The first is that you have the very real problem that any number, apart from zero, can represent either a positive or a negative number. Just as 9999 could be regarded as +9999 or -1 so could 0001 be regarded as +1 or -9999. How do you keep track of the pluses and the minuses? The best method is to divide up the number range into a section that you will regard as positive and a section that you will regard as negative. You can do this in any way that suits your purpose but mostly the division is done so that there are roughly as many positive as negative values. For example, with a four-digit decimal ten's complement system you might use 0001 to 5000 for positive values and 9999 (-1) to 5001 (-499) for negative values. This works well but notice that there is an anomaly contained in it. What is the negative of 5000? The answer is that in this system there isn’t one and 0-5000 in four-digit ten's complement should be considered to generate an “overflow” error. The second problem is how do you convert a value into its negative? You have to subtract it from 10^digits or in binary 2^bits and this implies that you can do such a subtraction. If you think that this is a little circular you would be right. The solution is another surprising simplicity of working in binary. As well as the ten's complement you can also define the nine's complement which involves subtracting x from 9999. You can use the nine's complement as a representation of negative values. It has some undesirable complications but is easy to compute in that each time you simply subtract each digit of x from 9 to get -x in nine's complement. Also as 9999 is just 10000-1 you can covert from a nine's complement to a ten's complement by adding one.
Tens complement
|
||||
| Last Updated ( Sunday, 25 June 2023 ) |