| Introduction to Boolean Logic |
| Written by Harry Fairhead | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Friday, 28 September 2018 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Page 2 of 4
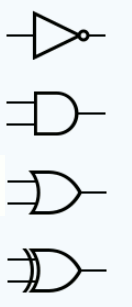
From Truth Tables to Electronic CircuitsNot only does this little demonstration illustrate why Boolean logic is useful in designing such systems, it also explains why electronics circuits to perform Boolean logic are commonplace. You can buy integrated circuits that perform And, Or and Not and many other combinations of these operations in a single easy to use package. Where is the “truth” in this? Clearly Boolean logic works with “true” and “false” and this is certainly how Boole himself thought about it, however you can work with the same system of operators and results no matter what you call the two states - up/down, on/off or zero/one. In the electronics case it is more natural to think of high and low voltage as representing the natural states that we are working with. An explanation that involves Boolean logic often sounds more appropriate when expressed in terms that belong to the underlying subject matter but it is still the same Boolean logic. What has all of this got to do with computers? The answer is two-fold. The first connection is that computers contain electronic circuitry that behaves in much the same way as the burglar alarm. In general Boolean logic helps when you need to design a circuit that has to give an output only when certain combinations of inputs are present. Such a circuit is called “combinatorial logic” and there are lots of them inside a computer. You can specify the behavior of any piece of combinatorial logic using a truth table. The only difference is that in most cases the tables are very large and converting them into efficient hardware is quite a difficult job. Logic in HardwareWhat makes Boolean logic so central to computers and a wide range of electronic devices is that logic is easy to implement. A logic "gate" is a piece of electronics that takes in some inputs and produces an output according to one of the logic tables. Usually the inputs are either high or low and this is interpreted as 1 and 0 or true and false. For example a Not gate has a single input and its output is high when its input is low and vice versa. You can create more complicated logic circuits by wiring up gates. The standad symbols for the three basic logic gates - Not, And and Or plus the exclusive Or are:
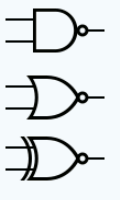
Note that the European standard symbols are different but in the main these have not caught on. In general a small circle on a connection indicates a negation or a not - see the Not gate. For example, the symbols for NAND, NOR and Not EOR or XNOR are :
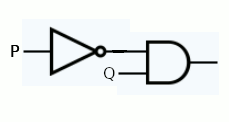
In many ways this is electronics made easy. You don't need to know anything about transistors or other components to build a logic circuit. Just work out what the logical expression is and wire gates up to implement it. For example, our burglar alarm example has the logical expression: R = Not(P) And Q So to implement it in hardware we need a Not gate and an AND gate:
Real logic circuits are much more complicated than this and can make use hundreds or even thousands of gates. Binary arithmeticThe second connection is actually just a special case of the first but it is very importan t and it often confuses people. Boolean logic can be used to implement binary arithmetic. Notice that there is no suggestion that binary arithmetic and Boolean logic are the same thing - they aren’t. Binary arithmetic is just an example of a place value system for representing values. That is, we humans work in base 10 and computers find it easier to work in base two because they don’t have ten fingers. However when you do binary arithmetic you follow standard rules that determine how you should combine bits together to produce result bits. These rule can be expressed as combinatorial logic - in other words a truth table. You can easily construct a table showing how to add two bits together to give a result and a carry to the next place:
If you don't know how to add two bits together then simply accept that the table as your instructions for how to do it. You can see that this is just another truth table and the combinatorial logic needed for it can be produced in the usual way. Actually this is only a half adder - yes this is the real technical term - in that it doesn’t add a carry bit that might have been generated by a previous pair of bits. The table for a “full adder”, this too is the correct technical term is:
So combinatorial circuits are the main connection between Boolean logic and computer hardware but there is more to computer hardware than combinatorial logic. Occasionally you will hear computers referred to just one huge piece of Boolean logic but this is an overstatement. Large chunks are just And, Or and Not gates but there are also huge chunks that are not describable in terms of pure Boolean logic. <ASIN:0965193403> <ASIN:1782050043> <ASIN:0471732788> <ASIN:0962781592> <ASIN:0071360573> |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Last Updated ( Friday, 28 September 2018 ) |