| Programmer's Guide To Theory - Practical Grammar |
| Written by Mike James | |||||
| Wednesday, 24 January 2024 | |||||
Page 2 of 4
Extended BNFTo make repeats easier you will often find that an extended BNF notation is used where curly brackets are used to indicate that the item can occur as many times as you like – including zero. In this notation: <variable> -> <letter> {<letter>}
means “a variable is a letter followed by any number of letters”. Another extension is the use of square brackets to indicate an optional item. For example: <integer constant> -> [+|-] <digit> {<digit>}
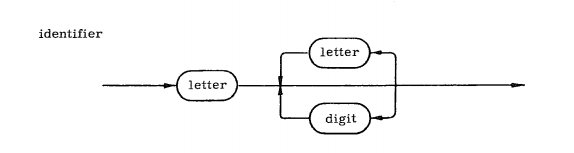
means that you can have a plus or minus sign or no sign at all in front of a sequence of at least one digit. The notation isn't universal by any means but something like it is often used to simplify BNF rules. If you know regular expressions you might recognize some of the conventions used to specify repeated or alternative patterns. This is no accident. Both regular expressions and BNF are capable of parsing regular languages. The difference is that BNF can do even more. See the previous chapter for a specification of what sorts of grammars are needed to model different complexities of language and machines. BNF in Pictures - Syntax DiagramsYou will also encounter BNF in picture form. Syntax diagrams or "railroad diagrams" are often used as an easy way to understand and even use BNF rules. The idea is simple - each diagram shows how a non-terminal can be constructed from other elements. Alternatives are shown as different branches of the diagram and repeats are loops. You construct a legal string by following a path through the diagram and you can determine if a string is legal by finding a path though the diagram that it matches. For example the following syntax diagram is how Pascal defined a variable name:
It corresponds to the rules <letter> -> <letter><letterordigit> <letterordigit>-><letter>|<digit> If you want to see more syntax diagrams simply see if your favourite language has a list of them. Here is a classic example in the 1973 document defining Pascal - scroll to the end of the pdf for the syntax diagrams.
Why bother?So what have we got so far? A grammar is a set of rules which defines the types of things that you can legitimately write in a given language. As such this is very useful because it allows designers of computer languages to define the language unambiguously. If you look at the definition of almost any modern language – C, C++, C#, Java, Python, Ruby and so on - you will find that it is defined using some form of BNF. However you will also find languages that don't bother. For example, the language PHP just sort of grew and was defined by its implementation. Only later did anyone go back and work out what the BNF needed to define it actually was. See - PHP Gets A Formal Specification For example, if you lookup the grammar of C++ you will discover than an expression is defined as: expression: Which in our BNF notation would be <expression>-> <assignment-expression>| As already mentioned, sometimes the BNF has to be supplemented by the occasional note restricting what is legal – for example no BNF grammar can restrict the length of a terminal string to a given number of characters. This use of BNF in defining a language is so obviously useful that most students of computer science and practicing programmers immediately take it to heart as a good method. This use of BNF in defining a language is so obviously useful that most students of computer science and practicing programmers immediately take it to heart as a good method. Things really only seem to begin to go wrong when parsing methods are introduced. Most people just get lost in the number and range of complexity of the methods introduced and can’t see why they should bother with any of it. |
|||||
| Last Updated ( Wednesday, 24 January 2024 ) |