| Cellular Automata - The How and Why |
| Written by Mike James | |||||
| Friday, 26 October 2018 | |||||
Page 3 of 4
Enter The GliderIn fact Life is so difficult to understand that even simple questions proved very difficult to answer. For example, are there any patterns which grow without end? In 1969 Conway discovered an interesting little pattern of five cells which he called a glider. Five cells that walk across the Life universe What made this interesting was that a glider walks its way across the Life universe and behaves like a basic particle that can be used to build other shapes. However the real breakthrough came in 1970 when, in order to win a $50 prize, Bill Gosper discovered the glider gun. This complicated arrangement of cells fired a new glider every 30 generations. At last it was proved that there were patterns which grew without limit because the gun added five cells every 30 generations. More important, however, was the fact that with a glider gun you could now begin to build machines in Life space! The streams of gliders could be used as if they were electric currents and thus logic gates and memory could be built. Soon a complete Life computer was constructed proving that the simple rule, involving only local behaviour of each cell, gave rise to a something as complicated as a digital computer. In other words, it was equivalent to a universal Turing machine that could compute anything that could be computed.
A glider gun – you can see two gliders moving off down and to the right After the glider gun, all sorts of interesting shapes were discovered – oscillators, movers, emitters and so on. The most important thing to notice is that even today Life is an experimental subject, very little if anything has been proved theoretically. What is more, Life is just one example of a range of similar cellular automata – each a simple collection of rules that invariably lead to complex behaviour. In general a CA is a universe of cells each of which can be in one of a number of states with the addition of a set of rules that depend only on the cells in the immediate neighbourhood of the cell. Given that these CAs are small artificial universes then you can see that we aren’t doing very well at explaining them. In our own universe we speculate that everything might well be based on some simple rule that generates all of the complexity, and hence we go in search of grand unified theories or a theory of everything. If we can’t find a theory of everything in situations when we know the rules then things look bleak indeed! There are lots of 2D CAs and indeed Life is just an example of a set of CAs called "Totalistic". In a totalistic CA the state of a cell is an integer which only depends on the sum of the states of its neighbours and possibly its current state. One dimensionThe problem with two-dimensional CAs, like the one described above and like Life, is that they are just too complicated to analyse in detail. The solution came from the mathematician Stephen Wolfram, whose first important contribution to the theory was to reduce the situation to the point where it could be analyzed. He decided that a one-dimensional CA would be worth investigating. The idea of a 1D CA is no different from a 2D one but we start off with a line of agents and at the next tick the line is replaced by a new line determined by the rule that is being followed. As this is only a 1D arrangement we don’t actually have to replace the existing line, just display the new line underneath, so building up a complete pattern of the development of the CA. It’s also possible to specify the rule in terms of the color of the agent, its two neighbors and the color of the new cell just below. For example the pattern:
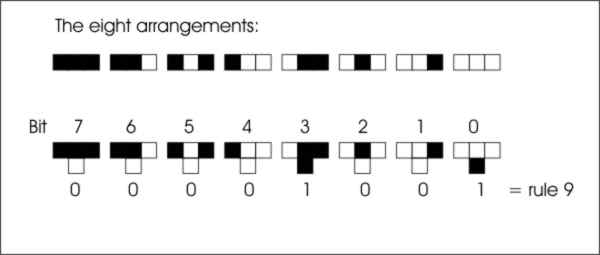
specifies a rule that if an agent is white and has two black neighbors then the cell below should be black. As there are only eight possible arrangements of neighbors a complete rule that specifies exactly what should happen in any situation only has to list if the result of each of the eight is black or white. By thinking of black as 1 and white as 0 you can give each neighbor pattern a number between 0 and 7 and then read off the resulting black or white cell on the next row as a set of eight zeros or ones, i.e. a binary number. This can be used as an index to specify the rule.
This means you can refer to any of the 256 rules that are possible in a 1D CA by number. This in itself is something of a conceptual breakthrough because now you can begin to think about classifying the behavior of each of the possible rules. This is exactly what a biologist would do when confronted by a new biosphere. Once you have classified what you are looking at you can start to see patterns and make theories up about what you are looking at. Without classification you are simply looking at an undifferentiated mess, no matter how interesting it might appear. |
|||||
| Last Updated ( Saturday, 03 November 2018 ) |