| Quick Median |
| Written by Mike James | ||||||
| Friday, 11 August 2017 | ||||||
Page 2 of 2
Divide and conquer in C#What is even stranger is that this is a 'divide and conquer' type algorithm and so it is likely to be fast. You can show that this method will (on average) find the median of n elements in a time proportional to 2n - which is much better than performing a full sort. An implementation of this median-finding method in C# might help understand exactly what is going on. The function split implements the scanning action. The n values are in the array a[ ], x is the splitting value, the left scan pointer is i and the right scan pointer is j. Notice that the two scan pointers have to be passed as ref because their updated values are used by the calling program to discover where they crossed.
do the left and right scan
Once the two scans stop we swap values if they are in the wrong part:
A function that makes use of the basic split method to find the median is:
This initially sets the scan to the whole of the array and x to the middle value. It then calls split repeatedly on appropriate portions of the array until the two pointers meet in the middle of the array when the value in a[k] is the median. Notice that this will only give you median if n is odd and it doesn't work at all if there are duplicate values in the array. If you are interested in finding percentiles other than the median then all you have to do is change the initial value of k. The value that you end up with in a[k] is always bigger than the number of element to its left and smaller than the number of elements to its right. For example, if you set k=n/3 then you will find a value that divides the array into 1/3rd, 2/3rds. Don't bother to use this algorithm unless the number of values is large. For small arrays almost any method will do and sorting is invariably simpler. Even when it isn't practical, this quick median method is always beautiful.
Listing
|
Advanced Hashing Hashing is arguably one of the great ideas of computing and it has hidden depths. Extensible hashing and perfect hashing are ideas that are worth exploring. |
What If Babbage..? What if the computer had been invented in the Victorian era? This isn’t a silly idea. Charles Babbage was born in the eighteenth century - the age of the Industrial Revolution. The calculating machi [ ... ] |
| Other Articles |
<ASIN:0132948443>
<ASIN:0262033844>
<ASIN:059651624X>
g the middle
by
Mike James
A friend of mine was writing a program to find the median. What's the median? The simple answer is that it is the value that is bigger than half of the values in a list. In a sense it is a middle value and it is important not only in statistics but also in lots of everyday programming tasks. For example, if you want to choose a value to split a set of elements in to two equal groups then the mean is the break point. The most obvious way of finding the median of a set of numbers is to sort the list into order and then look at the one half way down the list. The only trouble is that sorting isn't a very fast operation but at least the algorithm is simple and stable.
There is another way to find a median that is both fast and fascinating. If you are a collector of algorithms this is one you should have pinned on the wall. It was invented by C.A.R Hoare and is closely related to Quicksort another of his mind boggling algorithms. It is based on a partitioning method that moves elements of the array around to produce two regions - a left portion that is smaller than of equal to a given value x and a right portion that is larger than or equal to x.
---------------------
| <= x | >=x |
---------------------
You can think up lots of methods of partioning an array in this way but the simplest is:
1) start a scan off from the left of the array and stop when you find a value that isn't smaller than x. You know it is in the wrong place so remember where you got to and..
2) start a scan off from the right of the array and stop when you find a value that isn't bigger than x. You know it is in the wrong place so swap it with the value that you found in step 1.
Continue the scans from where they left off. When the two scans meet the array is correctly partioned - because ever element to the left of the where they met is smaller than or equal to x, it would have been moved if it wasn't and every thing to the right is larger than or equal to x for the same reason.
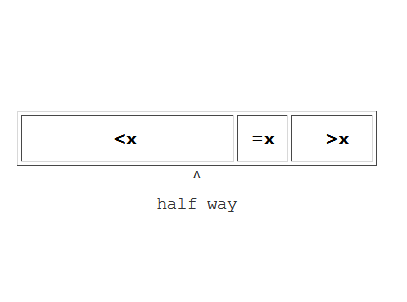
This partioning by scanning is a nice algorithm but what has it got to do with the median? Well imagine that you choose a value in the middle of the array and perform the scan. If by some change the two portions produced were of equal size x would be the median. That is if x is the median the partion is
---------------------
| <= x | >=x |
---------------------
^
half
way
Of course you would be very lucky to have found the median in the middle of the array and in most cases this wouldn't work. If x was smaller than the median then the two scans would cross before the middle of the array -
---------------------
| <= x | >=x |
---------------------
^
half
way
In this case you can pick the element that is now in the middle of the array (it must have changed but can you see why?) as a new value of x and repeat the procedure again but only on the right hand portion. You only have to re-partion the portion to the right because the portion to the left is already smaller than the new value of x - but can you see why?
If the initial value of x was bigger than the median the picture would be
---------------------
| <= x | >=x |
---------------------
^
half
way
and by the same argument you can pick the new element in the middle and repeat the partitioning but only on the left hand portion.
If you repeat this partioning process you will eventually find a pair of scans the do meet in the middle and the value of x is the median. I don't know about you but I get an uneasy feeling about this algorithm. If you really want to make sure that you understand the algorithm follow it to the point that you can understand how and why the value in the middle changes at each scan and why you only have to re-partion one of the portions. It is enough to keep you awake at night. Eventually the value stored at the middle of the array becomes the median and the values that it is bigger than or equal to are to the left an the values that it is smaller than or equal to are to the right. Very strange. What is even stranger is that this is a `divide and conquer' type algorithm and so it is likely to be fast. You can show that the this method will (on average( find the median of n elements in a time proportional to 2n - which is much better than performing a full sort.
An implementation of this median finding method in Quick BASIC might help understand exactly what is going on.
Subroutine split implements the scanning action. The n% values are in the array a(), x is the splitting value and the left scan pointer is i% and the right scan pointer is j%.
SUB split (a(), n%, x, i%, j%)
DO
DO WHILE a(i%) < x
i% = i% + 1
LOOP
DO WHILE x < a(j%)
j% = j% - 1
LOOP
IF i% <= j% THEN
SWAP a(i%), a(j%)
i% = i% + 1
j% = j% - 1
END IF
LOOP UNTIL i% > j%
END SUB
The first WHILE loop scans from the left and the second from the right. When two suitable values are found they are swapped over and the pointers are moved on past the values. The scan continues until the pointers cross.
The subroutine that makes use of split is
SUB median (a(), n%, k%)
l% = 1: r% = n%
k% = n% / 2
DO WHILE l% < r%
x = a(k%)
i% = l%: j% = r%
CALL split(a(), n%, x, i%, j%)
IF j% < k% THEN l% = i%
IF k% < i% THEN r% = j%
LOOP
END SUB
This initially sets the scan to the whole of the array and x to the middle value. It then calls split repeatedly on appropriate portions of the array until the two pointers meet in the middle of the array when the value in a(k%) is the median.
If you are interested in finding percentiles other than the median then all you have to do is change the initial value of k%. The value that you end up with in a(k%) is always bigger than the number of element to its left and smaller than the number of elements to its right. For example, if you set k%=n%/3 then you will find a value that divides the array into 1/3rd 2/3rds and so on.
Don't bother to use this algorithm unless the number of values is large. For small arrays almost any method will do and sorting is invariably simpler. Even when it isn't practical quick median method is always beautiful.