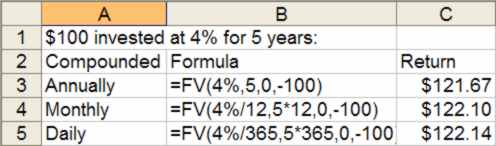| Simple and Compound Interest - Time Is Money |
Page 2 of 5
The value of moneySimple though this conversion to an annual rate is, it misses some important points. In particular, when interest is paid is also an important consideration in determining what it is worth. Payments made now are generally considered to be worth more than equal payments made in the future. This means that 12 monthly payments are worth more than the same total payment made at the end of the 12-month period. To understand the why and how of this situation we will have to look more carefully at the way time affects the value of money.
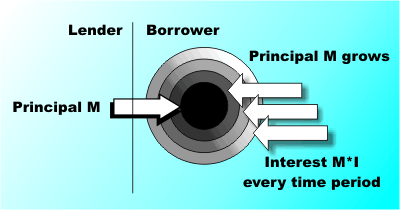
There is also the question of what happens if the interest affects the value of the principal. For example, you may choose to add the interest to the deposit or to increase the debt by deferring interest payments. This leads us on to consider compound interest. Compound interestMost people know that compound interest can exert powerful effects on the value of money, although stories involving a discovered inheritance generated by a small sum invested a long time ago are more often fiction than reality! Compound interest is at the heart of nearly all financial calculations and it is vital that you understand exactly how it works. Compound interest arises when the interest generated by a principal is added to the principal rather than being removed from consideration.
The only difference between an investment and a loan is that in the case of a loan the interest only notionally adds to the amount of money that the borrower actually has. However, this is irrelevant from the lender’s point of view because it certainly adds to the size of the debt!
The calculation for compound interest is remarkably simple as long as you have followed and understood the discussion of percentages in Chapter 1. If the interest is added to the principal this implies that the principal increases by I% in each period. To increase a value by I% you simply multiply by (1+I) and so at the end of the first period the principal, PV, has grown to:
At the end of the second period the principal has grown by another I% and so is given by:
and so on. After n periods the principal has increased to M multiplied by (1+I) n times over. If you repeatedly multiply by the same value n times this is called calculating a power. Mathematically this operation is indicated as xn. For example x3 is x*x*x. In the case of spreadsheets calculating a power is indicated either by x^n or x**n. So after n periods the principal is:
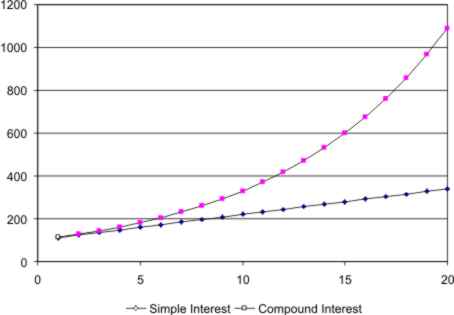
For example, an investment of $100 at 1% per month would yield a total of 100*0.01*12, i.e. $12, in one year if the interest were taken each month. If the interest was reinvested each month the total invested at the end of the year would be 100*(1+0.01)^12 which is $112.68, giving a profit of $12.68. After a single year the difference between simple and compound interest is a mere 68 cents. It hardly seems worth making the effort to do the calculation properly. However, the difference may start out being small, but compound interest acts to magnify these small differences over time. So for example, after 20 years the simple interest investment would have earned a total of $240, but the compound interest investment would have earned $989.25. The reason for the difference can be seen in the figure below, which shows a graph of the earnings for the two investments against time. You can see that the compound interest calculation causes the earning due to interest to increase each year. So the gap between the two widens, gradually at first, and then more rapidly.
Financial functionsIn the days before computers, calculations involving compound interest were considered to be very difficult. Working out powers and performing the necessary multiplications was time consuming and error prone. To reduce the burden tables and calculating approximations were often employed and an air of mysticism often surrounded financial calculations. With a spreadsheet however there is no need to to fear any calculation - working out a power is just as easy as a multiplication.
In most spreadsheets future value (FV) can be calculated using a function like:
where the principal is invested for n compounding periods at I% per period. Notice that there is a minus sign in front of PV. It is a convention that cash paid in (e.g. PV) is negative while cash paid out (e.g. FV) is positive. Don't worry about the 0 included in the function - in more complicated examples it represents any periodic savings you might make in addition to the lump sum initial value PV. For example, $100 invested for 5 years at 4% per annum produces a final balance of $121.67. The formula to type into a spreadsheet to calculate this is:
If you prefer to express the interest rate as a decimal fraction it becomes:
Notice the minus sign in front of the initial value. As explained earlier, this is because this represents cash that has been paid in. The above formula works out compound interest that is added on an annual basis. If you are being paid monthly interest you have to divide the annual interest rate by 12 to give a monthly rate and multiply the number of periods by 12 to give the number of months:
Similarly if interest is added daily the formula to use is:
The golden rule is that the interest rate must always be correct for the compounding period. In fact the compounding period can make quite a difference as shown in the figure which shows the formulas to enter as well as the results:
The effect of different compounding periods
<ASIN:047027560X> |