Solving for I, PV or n

The standard compound interest formula calculates the final balance produced when a given sum, the principal or PV, is invested at a given interest rate, I, for a given number of years, n.

Often this is exactly what you want to know, but sometimes financial questions are best put in terms of the interest rate or the investment term required.

For example, if I need a return of $1000 in 10 years time how much do I need to invest assuming I can secure an 8% interest rate for the full 10 years?

To answer this and other similar questions what we need are three other rearrangements of the standard compound interest formula to give n, I and PV respectively.

For such a simple calculation these formulas are surprisingly difficult to work out because they involve manipulating powers. However what really matters is what the formula are and this can be seen in the table below along with equivalent financial functions:

PV*(1+I)^n

=FV(I,n,0,-PV)

(FV/PV)^(1/n)-1

The only unusual component of the formulas given is the use of the ln (log natural) function in calculating n. If you haven’t encountered this function before don’t worry too much about it because all spreadsheets support the LN function so you can just use it.

To return to the problem at the beginning of this section, but slightly rephrased - what does PV have to be if FV is $1000, I is 8% per annum with interest added monthly and the investment period is 10 years? The answer is;

=1000*(1+0.08/12)^(-10*12)

or using the PV function:

=PV(8%/12,10*12,0,1000)

Both work out to be $450.52.

You can check this by working out the FV of $450.52 at 8% per annum calculated monthly for 10 years:

=450.52*(1+0.08/12)^(10*12)

or using the FV function:

=FV(8%/12,10*12,0,450.52)

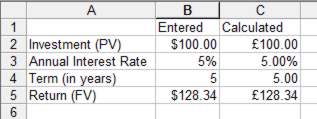
which gives $999.99 or thereabouts. The exact result depends on the number of digits precision that your spreadsheet works to - but 1 cent in $1000 in ten years isn’t an unacceptable error. 

An investment/loan spreadsheet

It is very convenient to have a spreadsheet that you can use to calculate the unknown fourth quantity involved in an investment or loan given any three of them. This is very easy using the formulas listed in the table above. Follow along to create this spreadsheet for yourself in Excel, LibreOffice Calc or as a Google Sheet so that you can experiment with different values or skip to the next section if you don't want the hands-on experience.

A column of entered values can be created next to a column of formulas that calculate each value from the remaining three. This description is easier to understand with reference to the screen dump below:

Enter the labels in column A and in B1 and C1 as shown, but do not enter any values in column B yet.

The following formulas need to be entered into column C:

Notice the need to multiply by 12 to convert the calculated monthly rate into a per annum rate and to divide by 12 to convert the term in months into years.

The final touch is to format B2:C2 and B5:C5 as currency and B3:C3 as percentage with two decimal places. Now when you enter any three of the values into column B the fourth will be calculated in column C.

Initially, because we have not typed anything in column B for the "Entered" values, when the spreadsheet attempts to work out the Calculated values, the resulting is a mix of zeros and error meesages.

This highlights a problem with this spreadsheet - as we only want it to work out one formula at a time the unused ones will show spurious results or suggest there are errors due to the incomplete data in column B.

The solution is to test if each entered value is zero and only calculate a value if it is, on the assumption that if the user hasn’t supplied one then it must be needed.This means surrounding the formulas in column C with IF statements that do the calculation when the cell to the left is zero and display a blank cell otherwise.

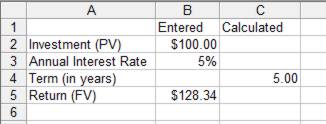
Now once three quantities are entered the remaining one will be calculated as shown below.

Enter PV, Interest Rate and FV and Term is calculated

An affordable loan

Although there is a tendency to think of this spreadsheet and its related calculations in terms of investment where the interest is re-invested, it is worth keeping in mind that it also applies to loans where the interest is `rolled up’ into the total debt to be repaid.

For example, if you know that you can afford to repay $1000 (and presumably make a reasonable profit) at the end of a 3-year project, how much can you borrow at 20% per annum.

Using the spreadsheet with FV equal to $1000 quickly gives the answer $551.53.

Inflation

Inflation is the gradual erosion of the purchasing power of money.

As this is usually reported as a percentage rate per annum it has many of the properties of compound interest. However while compound interest normally works to increase the size of the principal, inflation generally reduces the value of the principal.

For example, if inflation is running at 10% per annum, $100 held at the start of the year will be worth only $90 at the start of the next year. At this point it is tempting to use the simplistic argument that the $90 will be further reduced by $10 in the following year and so on until after 10 years there will be no value left at all!

This is clearly incorrect but it is surprising how often the argument is encountered.

The correct reasoning is. of course, that in the second year the value is reduced by 10% of $90, which is only $9 not a further $10 and so on..

You can see how inflation acts like compound interest in that the reduction in value affects the next time period’s calculation. To be more exact, after one year the value of $M is:

=M*(1-I)

after two years it is:

=M*(1-I)*(1-I)

and after n years it is:

=M*(1-I)^n

This is of course just the general formula for the FV under compound interest but with -I instead of +I. If we regard inflation as a negative interest rate then we can use all of the formulas listed earlier without change to calculate the effect of inflation.

For example, what will be the value of $100 in ten years time in today’s terms if inflation is running at 3% per annum? The answer is simply:

=100*(1-0.03)^10

or:

=FV(-3%,10,0,-100)

Both of these work out to $73.74.

That is, with 3% inflation, in 10 years time $100 will only buy what $73.74 will buy today.

Notice that in the case of inflation there is a potential for confusion over the use of the terms Future Value and Present Value!

There is a subtle point in the previous calculation that has been ignored so far. The annual rate of inflation may be quoted as 8% per annum but what is the compounding period?

The answer is that it depends on how the quoted rate has been calculated. Inflation is a process that happens continuously and so there is no sensible or reasonable compounding period to choose for calculations. (This point is discussed in more detail in Chapter 3). In most cases the quoted rate gives the correct results for an annual compounding period, hence the calculations above. This is often referred to as the “year-on-year inflation rate”.

<ASIN:1430218983>

<ASIN:0471779725>

<ASIN:0324407505> 

<ASIN: 0470037377>

<ASIN:1591397642>

<ASIN:0750681853>

<ASIN:0548862605>