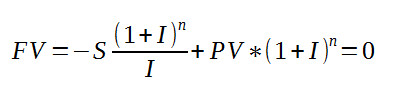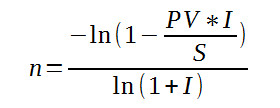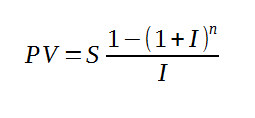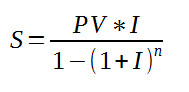| Cashflow Continued - Annuities |
| Written by Janet Swift | ||||
Page 2 of 3
Number of periods to zeroThe FV function can be used to give the balance after any number of periods but what usually interests us is not the balance after n periods but when will the balance be reduced to zero. The reason is that when the balance is reduced to zero the cash flow stops and thus this is the lifetime of the annuity. We can also ask other obvious questions such as given a sum of money and an interest rate how much can be taken given that the cash flow has to last n time periods. The first formula that we need is the number of periods it takes to reduce the Future Value to 0 -
solving this equation for n gives:
If this looks like an unappealing formula then you will be pleased to know that most spreadsheets supply a suitable financial function to make it unnecessary to struggle with the real thing. To calculate the number of periods needed to reduce the Future Value of an annuity to zero you can use the NPER function that has already been introduced but this time with the FV set to zero:
For example, how long will an annuity paying $200 with an interest rate of 10% and an initial deposit of $1000 take to exhaust the capital? The answer is:
which works out to approximately 7.27 years. If you use the FV function to work out the balance after 7 years:
you will discover that there is only just over $51 left in the account - not enough to pay the annuity in the following year. It this is a guaranteed annuity, i.e. one that is paid until the holder dies, then this is the point at which the annuity provider starts to make a loss. You can also see that with a table that gives the probability of dying, an actuarial table, you can easily work out the expected return on a guaranteed annuity. Present ValueYou can find the Present Value, i.e. the amount needed to be deposited to provide a payment S for n periods with interest rate I, of regular payments using the formula
Most spreadsheets provide a financial function to find PV
this gives the amount needed to generate a payment of S for n periods given and interest rate of I and leaving FV in the account at the end of n periods. Usually FV is set to zero because you need to know the minimum amount needed to fund the cash flow without leaving a residual sum in the account. For example, if you need a cash flow of $200 per month for 7 years at 10% per annum then the amount you need to deposit is:
which works out to -£937.68 which is a little less than the $1000 in the previous examples. Payments neededFinding the regular amount that can be taken given the value of the annuity and the interest rate produces a fairly simple looking formula -
In this case nearly all spreadsheets have a simple financial function that will work out payments. In most spreadsheets it is =PMT, the same one that works out the payments for a savings plan:
where Rate is the interest rate (which is normally denoted I in this book), nper the number of periods, PV (Present Value) is the initial deposit FV (Future Value) is the final sum of money in the account. For example, how much can you take for 7 years if the initial deposit is $1000 and the interest rate is 10% per annum:
which works out to $205.41, which again should be compared to the result given earlier that taking $200 leaves a little in the account after 7 years. The sum quoted reduces the account to exactly zero after exactly 7 years. Interest by iterationOnce again, as in the case of the savings plan, solving for I turns out to be impossible and iteration has to be used. In most cases you can find the interest rating using the function:
For example, if you take $200 for 7 years from an initial deposit of $1000 what interest rate to you need to make the final balance zero:
which works out to 9% per annum. |