| Linear Solver In Linear Time |
| Written by Mike James | |||
| Tuesday, 05 March 2013 | |||
|
Solving a general linear equation is more than quadratic in the size of the matrix, but if it has a particular form you can now do the job in nearly linear time. The breakthrough is not only faster, it is simpler and has lots of uses. A Symmetric Diagonal Dominant (SDD) problem is to find x in Ax=b with A such that its diagonal elements are larger than the sum of the magnitudes of all the non-diagonal elements in the matrix. That is, a SDD matrix is symmetric and has big diagonal elements compared to the rest. SDD matrix problems occur naturally in many situations - electrical networks, finite element models, computer vision and more. A slightly more specialized form of SDD matrix is the graph Laplacian. This arises from the study of graphs and it is the difference between the degree matrix D and the adjacency matrix A:
The degree matrix is simply a count of the number of edges incident at each vertex dii, i.e. it is a diagonal matrix. The adjacency matrix has the strength of the connection between vertex i and vertex j as its entries with the diagonal set to zero. The interpretation of what strength of connection means varies according to the subject. For example, for an electrical network the strength of connection is the conductance. The solution to the Laplacian problem is related to the flow through the network represented by the graph. It is difficult to see what the Laplacian has to do with anything when you first meet it, but it can be regarded as a discrete analog of the usual Laplacian operator. Consider for a moment a graph in the form of a rectangular grid with connection strengths set to one. Each vertex has four input edges and the so D is a diagonal matrix of fours and each row of A has four ones indicating the connections to the four neighbors. If you apply L, which is D-A, to a vector of ones each element of the vector is mapped to:
This is the usual discrete approximation to the 2D Laplacian operator. The Laplacian matrix is the generalization of the Laplacian operator to more general graphs. This identification between the Laplacian matrix, the Laplacian operator and the graph is an amazing and deep piece of math. What is important for this method of solution, however, is the connection between the Laplacian matrix and the structure of the graph. This is what is used to solve Lx=b in nearly linear time. It is worth pointing out that not all SDD matrices are Laplacians of some graph, but they can be transformed into a related Laplacian that then gives the solution to the original SDD problem. A group of MIT researchers, in a paper to be presented at this year's ACM Symposium on the Theory of Computing present a much simpler and faster algorithm than its predecessors. An earlier nearly-linear solution needed 130 pages and advances in spectral graph theory. The current method can be, according to its inventors, fit onto a blackboard. It is hoped that, as the method is so much simpler, it will be easier for practitioners to customize it to their needs.
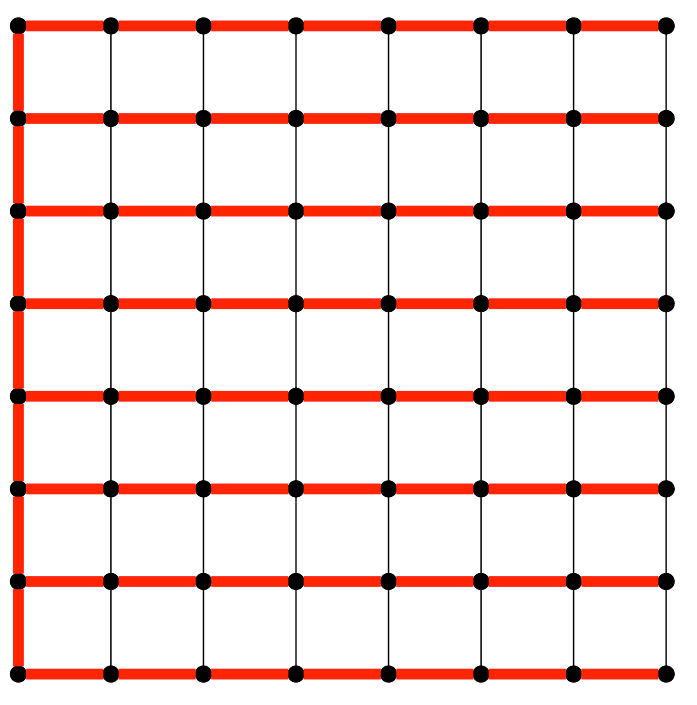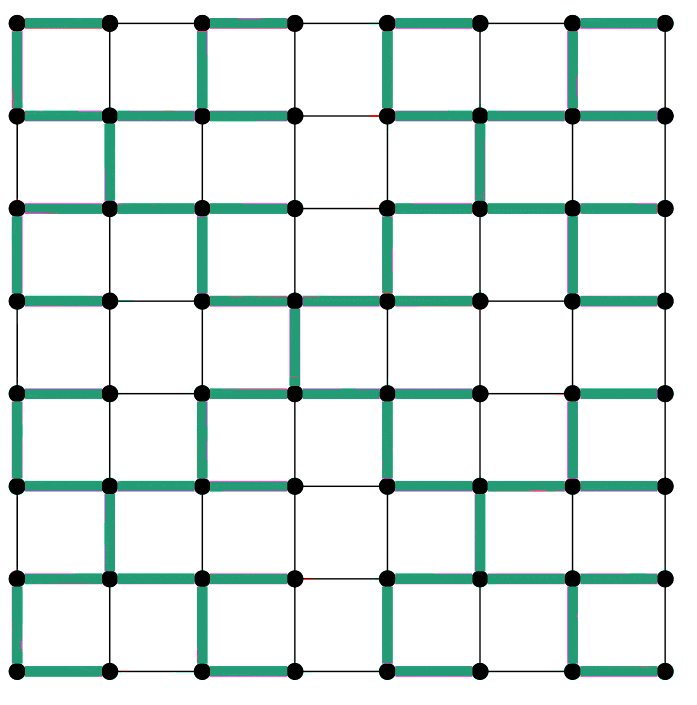
An example of a low-stretch spanning tree (green) v a non-low-stretch spanning tree (red)
The method works by finding a low-stretch spanning tree, i.e one that has short paths between vertexes, and then using this to generate a sparser graph. At each stage, the graph is solved to give the flow in the reduced network. A sequence of such graphs leads to the solution to arbitrary accuracy. It is worth noting that the solution isn't exact but the approximation can be made to any accuracy and the algorithm scales in close to linear time with m,n the size of the matrix: O(m log2n log log n log(ε-1)) You can read the details in the paper, but the important point it demonstrates is the remarkable connection between graph theory and linear algebra. It should also make it more practical to solve large linear SDD problems without having to move to a supercomputer. More InformationA Simple, Combinatorial Algorithm for Solving SDD Systems in Nearly-Linear Time Related ArticlesGoogle Zopfli - Nice Compression Shame About The Speed Network Coding Speeds Up Wireless by 1000% The XY Traveling Salesman Problem Solved
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Tuesday, 05 March 2013 ) |