| Programmer's Guide To Theory - Lambda Calculus |
| Written by Mike James | |||||
| Monday, 01 January 2024 | |||||
Page 2 of 4
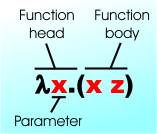
ReductionSo far we have a simple grammar that generates lots of strings of characters, but they don't have any meaning. At this point it is tempting to introduce meanings for what we are doing - but we don't have to. We can still regard the whole thing as playing with symbols. If this sounds like an empty thing to do, you need to remember that this is exactly what a Turing machine, or any computer, does. The symbols don't have any intrinsic meaning. When you write a program to compute the digits of π, say, you may think that you are doing something real, but the digits are just symbols and you add the extra interpretation that they are numbers in a place value system. There are a number of additional rules added to the bare syntax of the lambda expression that can be used to reduce one expression to another. The most important to understand is probably beta reduction. It is that if you have a lambda expression of the form: (λx.t) s then you can reduce it to a new lambda expression by replacing every occurrence of x in t by s and erasing the λx. You can think of this as a simple string operation if you like. For example: (λx. x z)(a b) is of the form given with t = x z and s = a b and so by beta reduction we have: ((a b) z) or dropping the parentheses: a b z
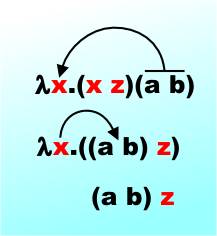
Reduction As Function EvaluationStarting from: (λx. x z)(a b) by our new rule we can replace the x in x z with s, i.e. a b. The resulting new reduced expression is:
You can think of this as a function application where the function is:
and
Hence when you write:
the function is evaluated by having the parameter x set to (a b) in the function body.
The only thing odd about this is that we don't usually write the parameter values after the function in this way. This, however, fits in with Reverse Polish Notation used in most functional languages. A very common example is the identity function:
which, if you think about its form, simply substitutes the expression you apply it to for x which gives you the original expression again. For example given:
then reduction means substitute (a b) for x in the function body which gives:
More than one parameterYou can have functions with more than one parameter by using more than one lambda. For example:
which means set z to the first expression (a b) and then set x to the second expression giving:
It is usual to abbreviate such multiple parameter functions by just writing a single lambda for all the parameters. For example:
which means z and x are the parameters for the function body x z. |
|||||
| Last Updated ( Wednesday, 24 January 2024 ) |