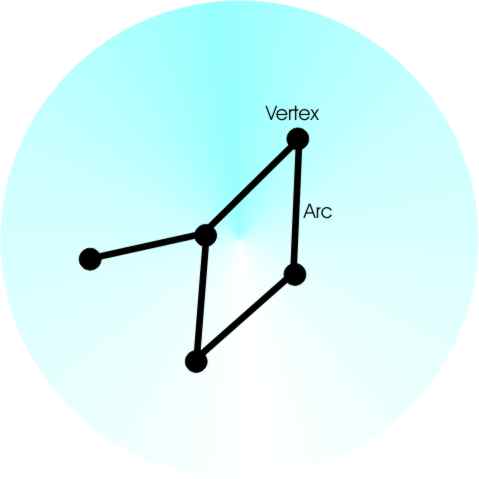
Finding the minimum spanning tree is one of the fundamental algorithms and it is important in computer science and practical programming. We take a look at the theory and the practice. 

Before we get started on the algorithm we need to find out what a minimum spanning tree actually is.

Graphs

In computer science and discrete mathematics a graph is a set of points – called vertices or nodes and a set of connecting lines called paths, arcs or edges.

This definition of a graph includes the familiar temperature charts etc but only as a special case. In this sense a graph is anything from a hierarchy chart to a computer network.

A simple graph of vertices and arcs

Graphs are important in computer science as a basic tool of theory and they are of practical importance.

Before we can go on to explain why we need some additional definitions:

• A path is a route from one vertex to another via arcs.
  
  
• If there is a path between every pair of vertices the graph is a "connected graph".
  
  
• A path from a given vertex and back again is called a cycle.

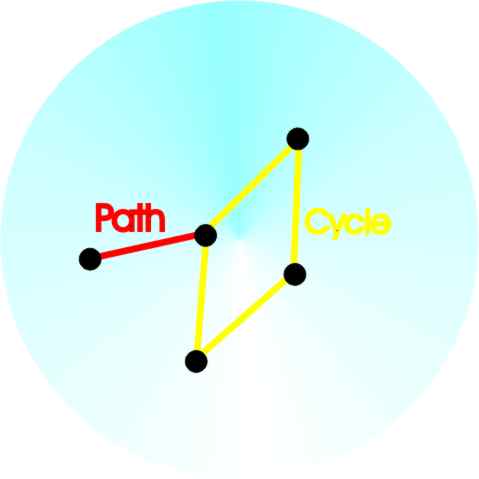
A connected graph showing a path and a cycle

Now we can define a tree – a tree is a connected graph with no cycles. There are many equivalent definitions of a tree including the one that gives it its name –  a root node connected to leaf nodes by branches.

Check that this is a connected graph with no cycles – aka a tree!

A slightly more advanced form of graph is the network. A network is a graph which has weights assigned to each of its paths. You can think of each weight as either being a distance or a cost associated with the path.

With networks you can ask questions such as "find the shortest path", "find the shortest round trip" and so on.

MST = Minimum Spanning Tree

One important version of this "shortest" type of question is – what is the shortest connector.

That is, the sub-graph with the shortest total distance that connects all of the vertices.

It doesn't take much to see the shortest sub-graph that connects all of the vertices is going to be a tree because if it contains any cycles you can get a shorter graph by deleting at least one arc without altering the connectivity.

As a result this problem is often called finding the "minimum spanning tree", MST.

Why is the MST important?

Consider the situation that you have to connect three computer sites into a network. All you care about is that every computer is connected and the cost of connection is proportional to distance. In this case the minimum spanning tree is going to be a good starting point for a practical implementation of the network.

Another, slightly more esoteric, example of the usefulness of an MST is that it provides an upper bound to the travelling salesman problem. The travelling salesman's round route has to be shorter than twice the MST for the network. 

Prim's algorithm

How do you find a minimum spanning tree given a network?

It turns out that there are two general algorithms – Prim's and Kruskal's.

Of the two Prim's is the easier to implement and to understand, so it makes a very good starting place to understand any graph algorithm. It is also an excellent example of a "greedy" algorithm, i.e one that always takes the best option at each step, that actually works!

This algorithm was developed in 1930 by Czech mathematician Vojtěch Jarník and independently in 1957 by computer scientist Robert C. Prim and was rediscovered by Edsger Dijkstra in 1959:

1.  Place all of the vertices in an "excluded" set and initialise an "included" set to be empty.
2. Select any vertex as the starting vertex of the tree. Place this vertex in the "included" set.
3. Find a vertex which is closest to any vertex in the "included" set. If there is more than one such vertex select one at random.
4. Repeat 1 and 2 until all of the vertices are in the included set and the excluded set is empty.

The result is a minimum spanning tree – as long as you remember to store which path between which pair of nodes was the shortest distance at each step!

Representing A Network

The above may seem simple but there are some interesting problems in implementing any graph algorithm using C#.

The first is how are we to represent a graph or network.

The simplest solution is to use a two-dimensional array to record the distance between each node. For example:

 Network[a,b];

would be used to store the distance between vertex a and vertex b. Notice that this matrix is symmetric and the diagonal is zero because the distance between "a" and "a" is zero.

The next problem is how to generate a network to try the algorithm out on?

In a real world problem the network would be entered as data to the array but it is a common requirement to generate valid examples of any data structure that a program is working with.

In this case the problem isn't difficult in that all we have to do is generate a set of random numbers between particular limits and make sure that the array is symmetrical and has a zero diagonal. This would produce a fully connected network which is difficult to represent graphically. To produce something that had fewer connections per vertex it would be necessary to set to zero entries picked at random.

While on the subject of representing the network graphically it is worth commenting that the distances in the network matrix don't have to be Euclidean distances. For example they might well be costs or subjective judgements. The algorithm works even if the distances aren't Euclidean but you can't draw the vertices in a 2D space with the given distances between them. This is a problem only if we want a to produce a graphical display – but in this case we do!

The solution is to work the other way around. First generate the vertices as random points in a 2D space and then work out the distances between them to store in the network matrix. If we also keep the locations of the points then drawing the network is even easier.

<ASIN:B09FTLPTP9>