| Rubik's Cube - The Order of God's Number |
| Written by Mike James | |||
| Wednesday, 29 June 2011 | |||
|
God's number is the smallest number of moves it takes to solve a general Rubik's cube. We still don't know the size of God's number for any cube other than the standard 3x3x3 but we do now know how it varies with the size of the cube and the remarkable thing is that it gets easier as the cube gets bigger.
Given we are in the business of creating algorithms you can't help but wonder how many moves are required in general to solve a Rubik's cube. To be precise we would like to know what has come to be called "God's number", i.e. the smallest number of moves needed to solve the worst possible cube. In the case of the familiar 3x3x3 cube it was proved that 20 moves are always enough to solve even the hardest mixup. Finding this result took 35 years of computer time. The next task is to find God's Number for generalized cubes - usually larger and so not as easy to solve using brute force enumeration. The question is how does the difficulty of the problem scale with the size of the cube?
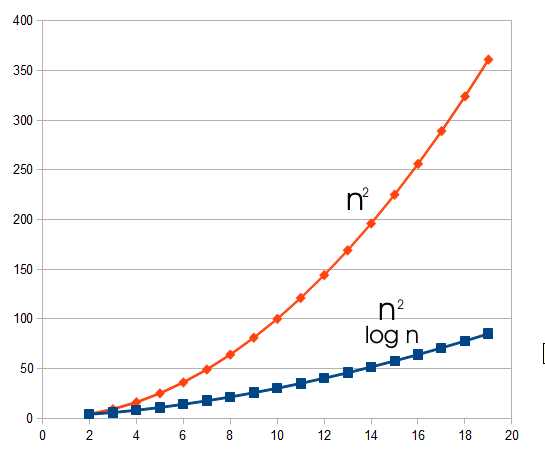
There is now an answer to this question in a paper to be presented at the 19th Annual European Symposium on Algorithms in September, written by researchers from MIT, the University of Waterloo and Tufts University. A dumb approach to solving the problem is to perform a set of moves that places a single sub-cube in its correct position and repeat until all the faces are complete. This gives an upper bound of order n^2 - as the number of sub-cubes all of the faces is proportional to n^2, However, it is well known that you can usually do better by using moves that place multiple sub-cubes into their correct location. These heuristics have now been made formal and this resulted in order n^2/logn being the new upper bound. Now this has also been shown to be the lower bound in the same paper. What this means is that the smallest number of moves required to solve the nxnxn Rubik's cube is proportional to n^2/log(n). Why is this surprising? Well the number of moves being proportional to n^2 is just a reflection of the fact that more surface faces mean more moves, but why is this reduced by log(n) as the size of the cube goes up? There have to be increasing numbers of shortcuts to the simple solution as the cube gets bigger. How n^2/log n varies with n and how much smaller it is than n^2
Notice that this result doesn't tell us God's Number for a cube of any size, only that it is proportional to n^2/logn. In addition the paper derives an asymptotically optimal solution for solving the general cube in the worst case. It also raises the question of whether finding an optimal solution to the general cube is NP hard or not. Algorithms for Solving Rubik's Cubes (pdf) See also:
<ASIN:1402753136> <ASIN:157912805X> |
|||
| Last Updated ( Sunday, 07 July 2024 ) |