| The Machine In The Ghost |
| Written by Mike James | |||
| Monday, 23 June 2014 | |||
|
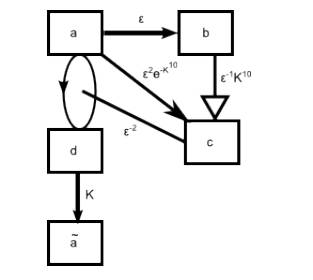
OK, the title really should be "the machine in the differential equation" but... A recent paper reveals that the clue to one of the seven most important problems in mathematics and what is more the approach suggests that computers might be hidden within physical phenomena. The Navier-Stokes equation models 3D fluid flow and hence it is important in a wide range of physical situations. However what isn't currently known is whether or not the solutions to this equation are "well behaved" in the sense of not blowing up by for example concentrating infinite energy at a single point in finite time. In other words is the flow described by the equation always going to be smooth? This is one of the Clay Millennium Problems along with PvNP and the Riemann Hypothesis - so you can see it is not only important but thought to be a tough nut to crack. The latest approach by Terence Tao, winner of the Fields Medal and recent recipient of the $3 million Breakthough Prize, doesn't solve the problem because it works with a simpler version of the Navier-Stokes equation which replaces it by an averaged version. In this case it seems that it is possible for the solution to blow up at a point. The way that this has been proved is interesting for the general theory of computation and perhaps even for Wolframs New Science theories. What Tao did was to construct "gadgets" within the rules of the equation that pushed more an more energy into a smaller space. The gadgets started out as logic gates within the fluid that could be assembled into increasing complex machines. With just five gates it proved possible to build a self replicating machine. Notice that this isn't a fluidic computer where the flows are contained within pipes but bundles of fluid withing the total bulk of the fluid.
One of the machines that in this case creates a delayed, but abrupt, transition of energy.
The flow is the computer. As Tao writes: "Somewhat analogously to how a quantum computer can be constructed from the laws of quantum mechanics, or a Turing machine can be constructed from cellular automata such as Conway’s “Game of Life”, one could hope to design logic gates entirely out of ideal fluid (perhaps by using suitably shaped vortex sheets to simulate the various types of physical materials one would use in a mechanical As well as having bearing on the future solution of the stability problem for the full Navier Stokes equations it might be relevant to Wolfram's idea of universal computation. This says something like - as long as a system is complex enough it is Turing complete and most natural phenomena are complex enough. In other words Turing complete computational systems are all around us. From this point of view it isn't particularly surprising to find a computer lurking in the complexities of a nonlinear differential equation.
More InformationFinite Time Blowup For An Averaged Three-Dimensional Navier-Stokes Equation A Fluid New Path in Grand Math Challenge Related ArticlesComplexity Theorist Gets Abel Prize A Mathematical Proof Too Long To Check - The Erdos Discrepancy Conjecture Search For Twin Prime Proof Slows A Computable Universe - Roger Penrose On Nature As Computation A New Computational Universe - Fredkin's SALT CA Cellular Automata - The How and Why
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Monday, 23 June 2014 ) |