| Best Laid Plans of Lions and Men |
| Written by Mike James | |||
| Sunday, 09 April 2017 | |||
|
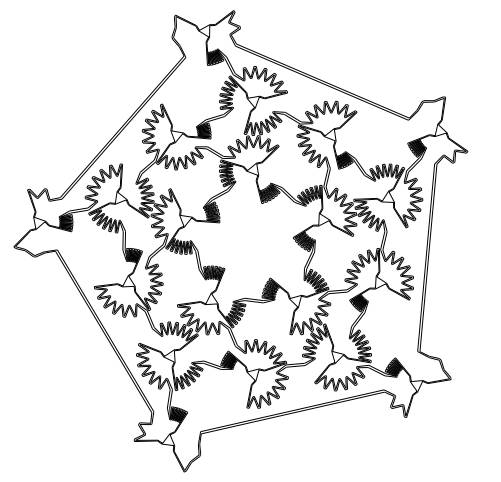
Can a man survive a lion attack by two lions? The answer is yes if the question is about mathematics and not real lions. This is almost a classic mathematical conundrum. The problem was originally posed by J.E. Littlewood, a famous mathematician. He was a friend of and collaborator with the even more famous mathematician, G.H. Hardy. The problem is a strange one, almost a game scenario. Take a playing area of a given shape, perhaps with internal holes where neither man nor lion can go, and see if the man can find an algorithm that avoids the lions for all time. The lions and the man are assumed to move at unit speed so it is more a game of geometric strategy than pouncing. There are a number of variations on the question. For example, a single lion and a single man in a circular arena. In this case an algorithm that evades the lion is known: Draw a line between the man and the lion. Run at right angles to this line for a set time. Repeat. You can prove that no matter what strategy the lion uses, i.e. what path it takes, the distance between the man and the lion is positive and therefore the lion never catches the man. However, if there are two lions in the circular arena the man cannot escape. In the case of the two lions and an arena of any shape with holes the solution wasn't known until the publication of a recent paper from a group of researchers from the Department of Computer Science at the University of Copenhagen, Denmark: We answer the following question dating back to J.E. Littlewood (1885 - 1977): Can two lions catch a man in a bounded area with rectifiable lakes? The lions and the man are all assumed to be points moving with at most unit speed. That the lakes are rectifiable means that their boundaries are finitely long. This requirement is to avoid pathological examples where the man survives forever because any path to the lions is infinitely long. We show that the answer to the question is not always "yes" by giving an example of a region Our construction is the first truly two-dimensional example where the man can survive. Next, we consider the following game played on the entire plane instead of a bounded area: There is any finite number of unit speed lions and one fast man who can run with speed So what does the 2D area look like? After all it might be important if you ever have to choose the arena in which you are to meet two hungry lions.
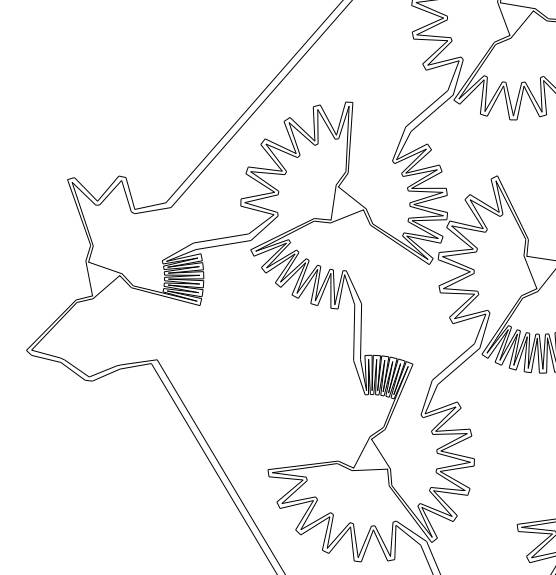
Well that isn't a simple shape! But it is even more complex than you might imagine. The description in the paper says: A region with 11 lakes in which the man has a winning strategy against two lions. The man and the lions are restricted to the triangular rooms and the narrow corridors that connect them. The narrow corridors correspond to edges of the dodecahedron and the triangular rooms correspond to vertices This is difficult to interpret until you enlarge the image:
Yes the accessible part of the region is more like a long wiggly corridor! The second result is also worth a thought. If you are pursued by a pack of any size, as long as it is finite, you can mange to avoid capture as long as you can run faster than any of the pack. So if you are pursued by a posse pick the fastest horse.
The paper is to be presented at SoCG'17, the 33rd International Symposium on Computational Geometry, taking place in Brisbane Australia in July. More InformationBest Laid Plans of Lions and Men Related Articles//No Comment - Turmits are Turing-universal, The Whale Swarm Algorithm & Rules That Govern Fish //No Comment - Approximate Edit Distance, Irrational Guards & DCT In 14 Additions Six Degrees Of Separation Is New
To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Sunday, 09 April 2017 ) |