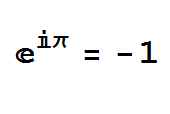The first three digits of Pi are 3.14 so March 14th is Pi day. This year no expense is being spared to make sure the world knows how fascinating this transcendental number is.

Every year at this time we are asked to give some thought to Pi but the real task is to get out there an enthuse some others, yes even arty types, about the amazing ideas that surround Pi.  It isn't enough to just say "Oh yes, it's the ratio of the circumference of a circle to its diameter." This much is just arithmetic, inconvenient arithmetic admittedly, but this is almost to trivialize the ideas that you need to master to comprehend what Pi is.

So here are some thoughts on Pi and a challenge to find ways of not only showing the uninitiated what they are about, but to actually find ways to let them see that this is more than arithmetic.

The first thing to say is that Pi is irrational - that is, you can't express it as the ratio of two integers a/b. This means that its decimal expansion goes on forever without falling into a repeating pattern - because a repeating pattern implies that you can find two integers with a ratio equal to Pi.

Next Pi is also transcendental, which simply means that there is no finite polynomial equation that Pi satisfies - which means there is no simple formula for Pi. Any formula has to be in terms of an infinite series.

From here things gets really interesting. What formulas can you find that give a good approximation to Pi? Notice that an infinite series for Pi gives an increasingly accurate result as you compute more terms of the series. So if you want the 56th digit of Pi you have to compute all the digits up to the 56th as well as the digit of interest - or do you? There is a remarkable formula - the Bailey–Borwein–Plouffe formula - which can provide the nth binary digit of Pi without having to compute any others.

The digits of Pi cannot be random - we compute them rather than throw a dice for them - but they are pseudo random. It is generally said that if you enumerate Pi for long enough then you will eventually find every number you care to specify and if you use a numeric code you will eventually find the any text you specify. So Pi contains the complete works of Shakespeare, or any other text you care to mention; the complete theory of QFT; and the theory of life the universe and everything. However, this hasn't been proved. Any number that contains any sequence if you look for long enough is called normal, and we have never proved that Pi is normal.

 Vi Hart is well known for her math videos and to celebrate Pi day we have a musing on finding Shakespeare in Pi and on the problem of proving Pi normal. If you listen, you will discover that it is in rhyme.

And here's another look at similar ideas, but not in rhyme:

 
The subtle ways in which Pi occurs in math in places where you can't see how circles come into the argument is also a reason we all love PI. - but perhaps the crowning glory is

Set your sights on explaining this equation and you get through a lot of math, a lot of physics and a lot of philosophy.

• Dr Mike James, founder and chief editor of the I Programmer website, is also the author of The Programmer’s Guide To Theory which, as its subtitle "Great ideas explained" suggests, sets out to present the fundamental ideas of computer science in an informal and yet informative way.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info

<ASIN:1871962439>

<ASIN:B081YS81L7>