| Speed Data Is Enough To Track You |
| Written by Mike James | |||
| Wednesday, 20 August 2014 | |||
|
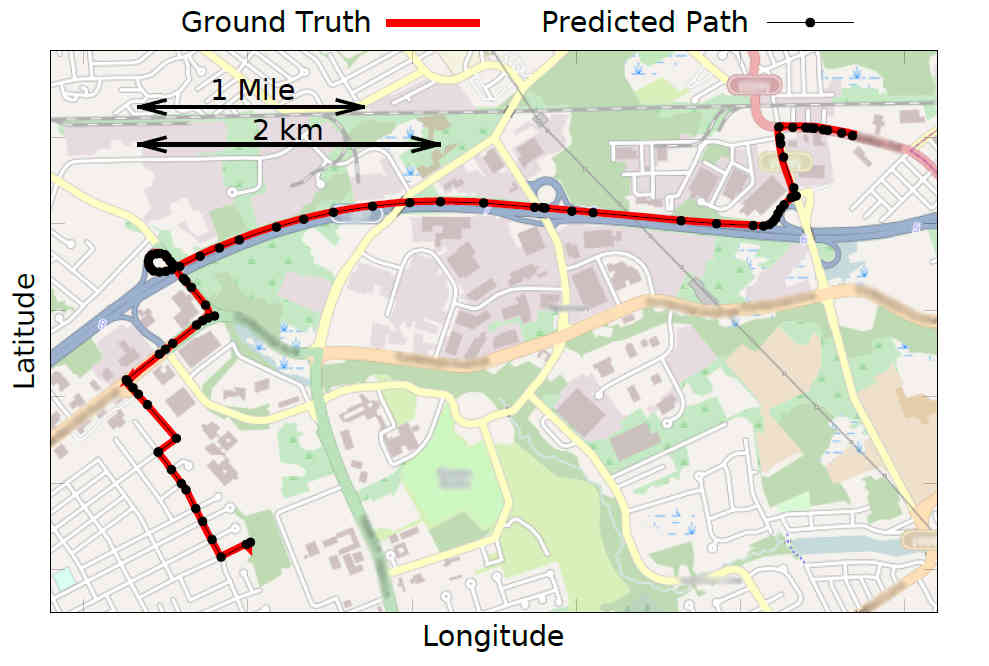
If I tell you how fast I have been driving and for how long, you might think that the best you can do is to compute the radius of the circle I must be in given my starting point. In fact, the data provides much more information than you might expect and it is usually enough to give your exact route. So tell me your speed and I'll tell you where you have been. Given that many insurance companies are offering lower rates to drivers who have data gathering boxes fitted that record speed and braking data, we need to know how much can be inferred from this data. The key idea is that different types of road correspond to different speed profiles. You have to slow down for some bends, stop at intersections, slow down to make turns and so on. This isn't the same as driving across a smooth flat plane where speed gives no clue as to location. By matching measured speed profiles to the ones suggested by different routes you can determine the route a driver took and their final destination. See it in operation in the video:
The algorithm used is called "elastic pathing" and has been created by researchers at Rutgers School of Engineering,. The basic idea is to work out how far the vehicle has traveled from the start location. Each time the vehicle reaches a junction on the map the number of possible paths increases. The match between the speed profile and each path is computed and the best path is the one that is displayed. The matching method that worked best was simply to take the road's speed limit plus 20 mph as the cut off for an impossible route. That is, if the actual speed is more than 20 mph above the speed limit the route is discarded as impossible. Of course, the driver could be breaking the speed limit by more than 20 mph but in the insurance monitoring case at least they should be on their best behavior. The algorithm is called "elastic" because it attempts to match by stretching portions of the data to fit sections of road to allow for inaccuracies. The position at the end of the path is pinned and the rest of the match proceeds from that point. This works to stop errors propagating by trying to pin down the exact position as the path is extended. For example, if there is a stop then this must be placed at the position of a junction and the path is pinned at this location even if the measured distance doesn't match exactly. Next the path is extended by taking each of the paths out of the junction and using the elastic method to fit the measured and predicted positions. Any paths that don't match are discarded.
The method isn't 100% accurate, but it is accurate enough to give a reasonble estimate of the route taken and the final destination. A variation of the algorithm could be used to rule out routes and destinations, which might be important for suspects in a court of law. Also repeated trips can be used to make the techique more accurate. Are there better algorithms that use additional data from the speed profile or create a better theoretical speed profile from map data? In the final analysis the source of noise in the process comes mostly from other traffic so perhaps finding a way to characterize this by the time of day, say, might help. Now you know how to keep your journeys hidden from a speed logging device - simply break the speed limit and do not stop at any intersections. I don't think that this will help you get a lower insurace rate, however. More InformationElastic Pathing: Your Speed is Enough to Track You Related ArticlesCat Photos - A Potential Security Risk? Smartphone Apps Track Users Even When Off PlaceRaider - Your Phone Can Steal A 3D Model Of Your Location Google Uses AI to Find Where You Live
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Wednesday, 20 August 2014 ) |