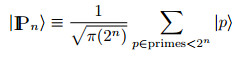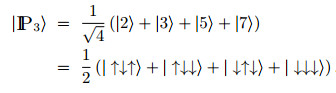| Solve The Riemann Hypothesis With A Quantum Computer |
| Written by Mike James | |||
| Monday, 25 March 2013 | |||
|
A new quantum algorithm allows the computation of a range of prime number functions to be computed well beyond the limits of a conventional computer. It is even possible that it could solve the million-dollar Riemann hypothesis. Quantum computers are all the rage, but they are very difficult to make. So far we have been able to build machines that small numbers of qubits - 4 or 5 - and the most high profile quantum algorithm, Shor's factoring, have only managed to factor the value 15 in practice. Given that to exceed the capabilities of conventional machines, a quantum computer would need to have about 1000 qubits we are still a long way from a successful real world application. So if you were looking for a potential real world problem for a quantum computer would you be looking for a simpler or a harder problem? As it turns out, the problem of computing various prime number functions is harder but, almost paradoxically, more promising for a real quantum computer. The best known of the prime number functions is π(x) which gives the number of primes smaller than or equal to x. Notice that this gives the distribution of the primes among all of the numbers and in this sense it is fundamental to number theory. The problem is that it is a difficult function to work out and currently we only know its values up to x=1024. The prime number theorem states that π(x)≈Li(x) as x gets large and Li is the logarithmic integral which is much easier to work out. The connection with the Riemann hypothesis is that if it is true then the difference between π(x) and Li(x) should be of the order √x log x. So, if you can experimentally show that the discrepancy is much larger than this, you can conclude that the Riemann hypothesis is false and claim the million-dollar prize from the Clay Mathematics Institute. To do this using a conventional computer would take a very, very long time and it is currently well beyond what we could hope to do. However José Latorre of the University of Barcelona in Spain, along with Germán Sierra of the Autonomous University of Madrid have constructed a quantum algorithm that can match the π(1024) using just an 80-qubit machine (i.e. you need about 80 bits to represent 1024). The key to the algorithm is the production of an entangled qubit state that involves just the primes.
For example for n=3 the state is:
where the arrows represent the spin states of each of the three bits needed to represent value from 0 to 7. The fact that such a state can be constructed at all is something of a surprise, but all it needs is the translation to quantum terms of classical primality testing algorithm. The example given uses the well known Miller-Rabin test to build a prime state. The idea is to use the Grover search algorithm with the primality test as the oracle to select just the prime elements from a superposition of all possible states. The final algorithm can construct the prime state in about √n operations and once you have the prime state it can be subjected to a quantum counting algorithm to produce π(n) or to other algorithms to produce related functions. Here we have a quantum algorithm that could provide us with new information using quantum hardware that is significantly smaller than for, say, the Shor algorithm. Notice, however, that this experimental approach can only disprove the Riemann hypothesis. If the findings agree with the Riemann hypothesis then this is not a proof, just a lack of a contradiction which may still exist for larger values of n. More InformationQuantum Computation of Prime Number Functions Related ArticlesBoson Sampling Tests Quantum Computing A Quantum Computer Finds Factors The Revolution In Evolutionary Game Theory - Prisoners Dilemma Solved? $100,000 Prize For Proving Quantum Computers Are Impossible
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Monday, 25 March 2013 ) |