| Vertex Coverings And The Cool Kids Problem |
| Written by Joe Celko |
|
Joe Celko has posed another puzzle that requires you to think like a programmer. This one asks us to find the cool kids in a social network - the ones who taken together know everyone else. This is also a classic problem in graph theory and it is NP-complete, something the cool kids probably don't know.
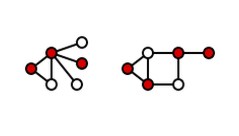
“Bugsy, are you back on Facebook at work again?” asked Melvin Frammis. Bugsy Cottman, a junior programmer at International Storm Door & Software, looked up from his keyboard, and said “Actually, I have a project from Jane Smith in Marketing, smart guy! I am having a little trouble understanding it.” “I do not Facebook myself", said Melvin, "but explain the problem to me, maybe I will see something.” Bugsy grabbed a piece of paper and draw some dots and connected them with lines. “The dots are people, the lines are friendings. We could give a free storm door to everyone to advertise our products, but that gets expensive.” “Is 'friending' a verb?” asked Melvin. “You just used 'Facbook' as a verb,” said Bugsy, continuing on. “We want to find the cool kids and market to them so that their friends will want to buy our storm doors. Let me use red dots for the cool kids, like this. Here are two sub-graphs and the cool kids:”
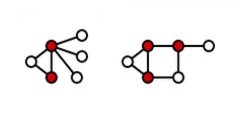
Notice that every edge in each of the graphs has an end terminating on one of the red dots. That is, there is no edge that doesn't end in a red dot. This is called a vertex cover of the graph. Notice that if you have a set of cool kids then, in a sense, you have the complete graph in that the cool kids are friends with everyone in the graph. This makes the cool kids an ideal target for marketing. “Okay, the red dots taken together are immediate friends with everyone in those networks.” said Melvin. “However, give me an eraser and that red pencil. Now we can re-color this graph. Now we only need two cool kids in the first network and three in the second one.”
This is a minimum vertex cover for the two sub-graphs in that with any fewer red dots there would be edges that didn't have an end terminating in a red dot. Starting from any vertex cover you can manually prune the red dots until you reach a smallest set. “Exactly! You can do these two graphs by hand, but how do I do the general case? And at least get close to the smallest set of cool kids?” “Mmm, I have the horrible feeling that this is going to be one of those problems where you have to try all the combinations.” said Melvin. “But let's back up and decide how we want to model a network. Let's number the nodes from 1 to some (n), show the edges as pairs of (x, y) where (x <> y) and if we have (x, y), then we have (y, x) in the set ...” “That is about as far as I got, too.” said Bugsy. “But I can make it worse. Look at those two cliques. Right now they do not talk to each other. But what if I introduced two people from different social networks? Do I need to re-color the combined graph?” “I guess we need to start with Google for help.” said Melvin. “But we are programmers, so why don't we generate a random network and see if we can write something to at least find one subset that covers all the nodes?” That is your assignment, readers! Notice that you do not have to generate a minimal vertex cover but it does have to be a true subset of the nodes, i.e. it isn't enough to find the trivial vertex cover consisting of all the nodes in the set. The formal definition of a vertex cover is: a set of vertexes such that each edge of the graph is incident to at least one vertex of the set. A minimal vertex cover is a smallest such set. You can prove that this problem is NP-hard in its decision version.
If you would like to send in a complete solution to this puzzle email editor@i-programmer.info. Or use the comments below to discuss how to approach it. If you would like an academic view of the problem then this video is an extract from: Algorithms Specialization on Coursera Course 2 Graph Search, Shortest Paths, and Data Structures.
Joe Celko is best known as the database expert who writes books on SQL, data and databases. But before that, he was an honest developer obsessed with finding good algorithms and clean code.
More PuzzlesSharpen your Coding Skills - Elevator Puzzle
Comments
or email your comment to: comments@i-programmer.info
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
|