| Database The Prolog Way |
| Written by Mike James | |||||
| Friday, 18 February 2022 | |||||
Page 2 of 4
Begin PrologIn Prolog you can write statements of fact using an abbreviated notation. For example, you can write
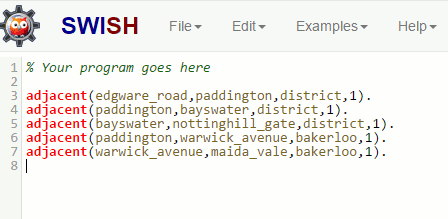
to mean the son of Mary is David. In Prolog this sort of statement is known as a 'clause'. You should be able to see that this is very similar to a record consisting of two fields - mother's name and son's name and indeed the simple clause does play the role of a record in Prolog. In the case of the Underground network problem the information to be stored concerns which stations are connected. The form of clause used to hold this information is
which records the fact that station1 is adjacent to station2 on tube line 'line' and it takes 'time' seconds to get from one to the other. For example,
means that after Wembly Park Preston Road is the next stop on the Metropolitan line and it takes 4 minutes to get there - facts you can check using the tube map. You should be able to see that it is possible to represent the entire underground system as a large collection of adjacent clauses. And to try things out start SWI Prolog or use the in browser editor and use the File, New command to create a new file called Route. Using the editor enter the following:
If you are using the online version type into the left hand window. You also need to remember to type the full stop at the end of each clause which acts as an end of clause marker.
So far we have very little that is new because the collection of adjacent clauses is equivalent to a database consisting of records with fields station1, station2, line, and time. However if you compile this "knowledge base" you can already do some things that are beyond a simple database.
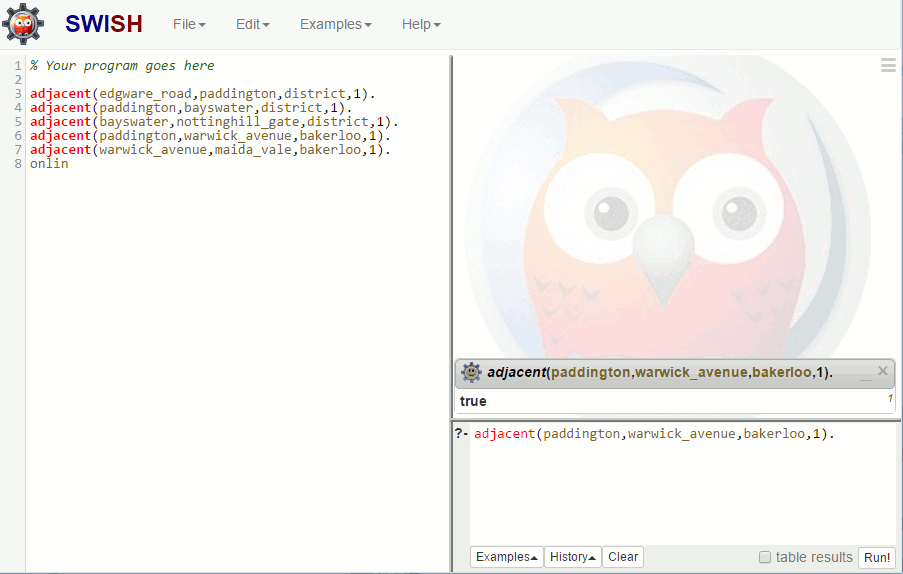
Some QueriesIf you are using the downloaded compiler you use Compile,Compile Buffer in the editor. Provided this finds no errors it adds the compiled code into the runtime and you can interact with it using the main SWI Prolog window. If you are using the online version you don't have to compile anything as it is done for you. To interact with the "data" you simply type into the query window which is at the bottom right. Switch from the editor to the main/query SWI Prolog window. Here you can type in "live queries" i.e. anything you type in will be immediately evaluated as true or false. To indicate that you have finished a query you type a full stop. For example, if you type in:
the system will display
Because this is a "fact" you have included in the database.
If you type in
it will return the result
because that fact is not in the database. So far so good but not impressive. Searching For UnknownsNow try:
in this case the system comes back with:
Now this should be more impressive. You have specified two "variables" X and T and the Prolog system has searched through the clauses to find values of X and T that make the query true. If it couldn't find such values then it simply fails and returns false. Yes - Prolog contains a built in search algorithm. In fact the search algorithm is quite sophisticated and able to use rules and clauses to find values that satisfy complicated queries. The question of how to get from one station to another is one such query. To answer it you would have to know and be able to apply the simple rule that every human knows about connectivity - If A is connected to B and B is connected to C then A is also connected to C Using this rule you could scan through the database and build up chains of stations that were adjacent and that formed a route between the starting and finishing stations of your journey. This is not something that most databases can manage easily but in Prolog you can state the connectivity rule as
This simply says that station X is connected to station Y if there exists a station adjacent to X that is connected to Y. Where the comma between the two is read as And. The underscores simply mean that we don't care what the values of something are. This isn't quite all we need because connect is defined recursively and we need a case to stop the recursion. Two stations are obviously connected if they are immediately adjacent:
This rule defines the simplest meaning of connected. Prolog will try to find values of X, Y and Z that make the clause true. If you enter the connect clauses into the database you can try out the query:
Notice that the two stations are not directly connected but Prolog works out that they are connected by and intermediate and prints true. You will also notice that it prints false as well in the online version. This is because it also reports results of searches that fail. Notice that there is more going on here than you might think. The Prolog program as written will discover that:
is true. Notice that to do this it has to find the chain
That is it has had to find two intermediate stations. Also notice that there is at least one route starting at edgware_road that doesn't lead to maida_vale. What this means is that Prolog not only has a simple search built in but a search which can backtrack when it initially goes the wrong way. The online version gives you information on these "back tracked" searches. <ASIN:013138645X> <ASIN:3540629718> <ASIN:1432749366> <ASIN:0262514451> <ASIN:3540006788> |
|||||
| Last Updated ( Friday, 18 February 2022 ) |