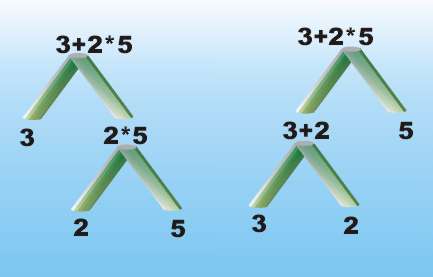
Syntax is semantics

So in natural languages syntax carries with it some general indications of meaning.

The same is true of the grammar of a programming language.

Consider a simple arithmetic expression

3+2*5

As long as you know the rules of arithmetic you will realize that you have to do the multiplication first. Arithmetic notation is a remarkably sophisticated mini-language which is why it takes some time to learn in school and why beginners make mistakes.

Implementing this arithmetic expression as a program is difficult because you can't simply read it from left to right and implement each operation as you meet it. That is 3+2*5 isn't (3+2)*5 but 3+(2*5) the multiplication has a higher priority.

A simple grammar for this type of expression, leaving out the obvious detail, might be

<expression> -> 
  <expression> + <expression> | 
    <expression> * <expression>

This parses the expression perfectly but it doesn’t help with the meaning of the expression because there are two possible ways that the grammar fits –

<expression> -> 
    <expression 1>+<expression 2> 
         3        +     2*5

or

<expression> ->
    <expression 1>*<expression 2> 
         3+2      *      5

These are both perfectly valid parses of the expression as far as the grammar is concerned but only the first parsing groups the expressions together in a way that is meaningful.

We know that the 2 and 5 should group as a unit of meaning and not the 3 and the 2 but this grammar gives rise to two possible syntax trees –

We need to use a grammar that reflects the meaning of the expression.

For example, the grammar:

<expression> -> 
  <multi–expression> + 
             <multi-expression>
<multi-expression> -> <value> * <value> |
                                   <value>

also allows 3+2*5 to be legal but it only fits in one way:

<expression> -> 
  <multi-expression> + <multi-expression>
           3         +        2*5

<multi-expression> -> <value> * <value>
                         2         5

This means that this particular grammar only gives the syntax tree that corresponds to the correct grouping of the arithmetic operators and their operands.

In this case we have a grammar that reflects the semantics or meaning of the language and this is vital if the grammar is going to help with the translation.

There may be many grammars that generate a language and any one of these is fine for generating an expression or proving an expression legal but when it comes to parsing we need a grammar that means something.

Travelling the tree

Now that we have said the deeply unfashionable thing that syntax is not isolated from semantics we can now see why we bother to use a grammar analyser within a compiler.

Put simply a syntax tree or its equivalent can be used to generate the machine code or intermediate code that the expression corresponds to.

The syntax tree can be considered as a program that tells you how to evaluate the expression.

For example, a common method of generating code from a tree is to walk all its nodes using a “depth first” algorithm.

That is, visit the deepest nodes first and generate an instruction corresponding to the value or operator stored at each node. The details of how to do this vary but you can see the general idea in this diagram.

So now you know. We use grammar to parse expressions, to make syntax trees, to generate the code. Now find out about different types of grammar and parsing methods – they are important.

Further reading:

Assemblers and assembly language

The Heart Of A Compiler

John Backus - the Father of Fortran

Brackets are Trees

Finite state machines

Turing Machines

A Concise Introduction to Languages and Machines

Language Implementation Patterns

The Universe as a Computer

To be informed about new articles on I Programmer, subscribe to the RSS feed, follow us on Google+, Twitter, Linkedin or Facebook or sign up for our weekly newsletter.

<ASIN:1848001207>

<ASIN:0465030793>