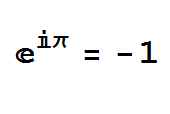| Pi Day 2017 - Why Pi? |
| Written by Mike James | |||
| Tuesday, 14 March 2017 | |||
|
It is Pi Day again and it's time to think deep thoughts about Pi and why it is so special. Of course, you can just use it as an excuse for eating large amounts of Pie.
Pi Pie, created at Delft University of Technology, applied physics, seismics and acoustics
Assuming you are reading this on the 14th of March then the good news is that it is Pi Day. Of course, the date has been chosen because it is 3/14 i.e. 3rd month, 14th day, and these are the first three digits of Pi, 3.14. There is an argument that as 22/7 is a close rational approximation, we should have another Pi day on the 22nd July in countries where we write dd/mm. Why is Pi so important? There are just so many reasons. Note: I'm going to avoid precise math in what follows just to give you some feeling for Pi. Pi is an irrational transcendental number and this makes it sound attractive even to non-math types. In fact, it makes it sound attractive to nut cases and romantics alike. It is an irrational number because it cannot be expressed exactly as the ratio of two integers, aka rational numbers. There are mathematicians who are of the opinion that all our problems started when we invented irrational numbers and admitted them into mathematics. You can express irrational numbers in many different ways but, as a decimal fraction, an irrational number can never fall into a repeating pattern. The reason is that if you find the number settles down into a repeating pattern, no matter how long, the you can reduce it to the ratio of two integers and it is rational. So Pi is a decimal number that never comes to an end and never falls into a repeating pattern. The transcendental aspect just means that there is no finite polynomial that Pi satisfies. This means that there is no finite simple equation that Pi is the solution of and any formula for Pi has to be an infinite series. As you can see, for something that is just the ratio of the circumference of a circle to its diameter, Pi seems to have a lot of infinities buried in it. But wait there is more to Pi than just this. Pi has a computational aspect and we are programmers so this is the important part from our point of view. What is mainly wrong with the irrationals is that there are just too many of them. You can easily show that there are more irrationals than there are programs to compute them. Technical aside: programs are binary numbers, i.e. integers, and there are only a countable number of integers. Irrationals are uncountable and so there are more irrationals than integers and hence programs. See:The Programmer's Guide To The Transfinite What this means is that nearly all irrational numbers are non-computable. There are no computer programs that output them. In fact not only are there no programs that output them this implies that we don't even have proper names for them - there being more irrationals that available labels. The ones that do have "names" are the algebraic numbers because they satisfy equations and we can treat the equation as the name of the number. For example: x^2=2 is the name of the square root of two which is irrational, but algebraic, not transcendental. That is, most irrational transcendentals aren't computable and we don't have names for them. So now you see why Pi is special. It is, however, not the only irrational transcendental that we have a name for - think of e or ... well after that it gets quite hard to think of well-known transcendentals. If you try really hard there's Euler's constant gamma, Catalan's constant and perhaps Feighenbaum's number. Of course, there is no shortage of transcendentals as espressions that contain transcendentals often turn out to be transcendental - for example 2*Pi is transcendental. Not every expression that involves a transcendental is transcendental, however. The famous e to the i Pi equals -1 shows that a transcendental raised to a transcendental power can be an integer.
So Pi is a transcendental that we have a program for in the sense that there is a finite program that will compute Pi to any precision in a finite time. Pi is special in the sense that, as well as being computable, it is very computable in that there is a program that will get you any digit of Pi without having to compute all the others that lead up to it. It is also conjectured that it is a normal number in that because it goes on forever and never falls into a repeating pattern, basically every number sequence you can think of has to be in there somewhere. This is the basis for those websites that will tell you where your birthday is in the digits of Pi. Also notice that you could use Pi as a cipher or a compression algorithm by giving the starting digit and length of any sequence you wanted to send. For example, 234569321,1000 is the 1000 digits starting at the 234569321th digit of Pi. To use it you just need to be able to find digit sequences in Pi. The bottom line, in vague and nontechnical terms, is that Pi is special because most transcendental numbers resemble random strings of digits, but Pi has a deep inner regularity that makes it very computable if not quite regular enough to be an algebraic irrational. Happy Pi day.
More Informationhttp://en.wikipedia.org/wiki/Pi_day Related ArticlesThe Life Of Pi - Yes It's Pi Day Celebrate Pi Day It Contains All Human Knowledge Non-Computable And Other Numbers Normal Numbers - A Video In Rhyme ComputabilityConfronting the unprovable 60 trillionth binary digit of pi-squared calculated Yahoo! Gets to the 2 Quadrillionth bit of Pi - it's zero The Programmer's Guide To The Transfinite
To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Thursday, 14 March 2019 ) |