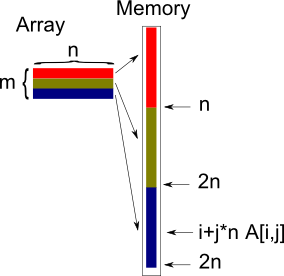You may not have heard of SMFs, Storage Mapping Functions, but you are likely to have used them. They tend to be overlooked because there are more exciting methods of implementing storage, such as hashing schemes, but really it all started right here with an SMF and there is a sense in which all exciting stuff is just SMFs reinvented. 

What Programmers Know

Contents

1. The Computer - What's The Big Idea?*
2. The Memory Principle - Computer Memory and Pigeonholes*
3. Principles of Execution - The CPU
4. Assemblers and assembly language*
5. The Essence Of Programming
6. Variables - Scope, Lifetime And More*
7. Binary Arithmetic
8. Hexadecimal*
9. Binary - Negative Numbers*
10. Floating Point Numbers*
11. Inside the Computer - Addressing
12. The Mod Function
13. Recursion
14. The Lost Art Of The Storage Mapping Function *
15. Hashing - The Greatest Idea In Programming
16. Advanced Hashing
17. XOR - The Magic Swap*
18. Programmer's Introduction to XML
19. From Data To Objects*
20. What Exactly Is A First Class Function - And Why You Should Care*
21. Stacks And Trees*
22. The LIFO Stack - A Gentle Guide*
23. Data Structures - Trees
24. Inside Random Numbers
25. The Monte Carlo Method
26. Cache Memory And The Caching Principle
27. Data Compression The Dictionary Way
28. Dates Are Difficult*
29. Sequential Storage*
30. Magic of Merging*
31. Power of Operators
32. The Heart Of A Compiler*
33. The Fundamentals of Pointers
34. Functional And Dysfunctional Programming*

* Recently revised

A Necessary Skill

Back in the bad old days when languages were primitive and programmers had to punch cards, most knew about the academic sounding Storage Mapping Functions or SMFs.

In these days of data abstraction and encapsulation SMFs are less well known, but just as useful. In fact they are so important that you probably use the technique often without even realizing it and without knowing that it has a name. 

A storage mapping function is simply a function that gives the location in memory where something is stored. 

If you want to be abstract, then a SMF is a function F that takes a key i.e. something determines the data you want and returns the location of the data:

locationOfData=F(key);

The nature of a storage mapping function changes according to the type of key used and, of course with the type of storage in use. 

Storage mapping functions were probably invented when programmers first needed to implement the one dimensional array. 

For example, an array of two byte integers can be implemented using the simple SMF:

location = base + 2*index

where base is the starting address of the array.

This works simply because the first array element is stored at base, the next is at base+2, the next at base+4 and in general the ith element is stored at base+2*i.

In general a one-dimensional array composed of elements that each occupy b bytes can be implemented using the SMF:

location = base +b*index

Obviously to find the location of a[i], assuming that you have decided to call the array a, all you have to do is work out base+b*i and then retrieve or store the value associated with a[i] there. Notice that this implies that the first array element is a[0] as when index=0 location=base i.e. the start of the array.

If the first array element is considered to a[1] then you have to work with i-1 making the SMF

location = base +b*(index-1)

You can argue that this is the reason that most arrays start from an index of zero - it avoids the messy subtract 1. 

This really is how assembly language programmers did the job.

They didn't have arrays - they have to structure the storage they had using SMFs. Given the address of a block of memory then the SMF was used to work out where to store a value and where to retrieve it. 

If you know C you might just recognize the way pointer arithmetic works with arrays as being just a formalization of the array SMF. 

Into 2D

SMFs for one-dimensional arrays are a bit too simple to be interesting but at least they make good examples.

The same principle however applies to two-dimensional arrays.

A two-dimensional array a[i,j] or a[i][j] of b byte elements with dimension n by m can be implemented using the SMF:

location = base + b*i + b*n*j

It is also assumed that the array indices all start at 0, if not then simply change i to i-1, and j to j-1 etc. 

The same idea can be extended to as many dimensions as you like but its when you get to 2D arrays that the meaning of a SMF starts to become clear. What you are doing is finding a function that maps the structure of the data onto a linear storage system. In the case of the 2D array you have a table and its rows are mapped onto linear storage one after the other:

Bitmaps And Stride

This is also the SMF used to map pixel data into linear storage be it memory or a file. If you have a bitmap stored in a byte array with nxm pixels and each pixel takes bpp bytes to store the pixel at x,y is stored starting at:

pixel=x*bpp+m*y*bpp
      =(x+m*y)*bpp

The only complication in the case of a bitmap image is that sometimes the length of a row has to be a multiple of four or some other value. In this case the length of a row isn't just the size given by the bitmap's dimensions. That is the row is padded beyond the m pixels to make it a multiple of what ever number is specified. The physical storage size of a row of a bitmap image is usually referred to as its "stride".

This makes the SMF:

pixel=(x+stride*y)*bpp

There are lots of other cases where you need to map a 2d structure onto a line and the same SMF is used with minor changes.

If you need to map a n dimensional structure onto a line then the same sort of formula works. For example suppose you have a cube of data n by m by p. Then you are going to store the data in row order and add the number of columns and the number of pages. So to find C[i,j,k] the SMF is:

location = i + n * j + n*m*k

If it takes b bytes to store an element then you multiply the SMF by b. 

The n is just the number of elements in a row and the n*m is the number of elements in a page. The same general method works for any dimension.  

<ASIN:3540779779>

<ASIN:0521880378>