| What's a Sample of Size One Worth? |
| Written by Mike James | |||
| Monday, 25 June 2012 | |||
|
We are in the information business and it seems obvious that more data is better, but how much better? Would you be surprised to learn that most of the information is in a single measurement?
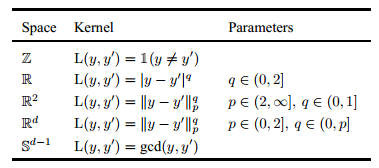
The Cover-Hart inequality was introduced to the world in 1967 but few people seem to know of it or its implications. If you are a statistically-oriented programmer doing data mining or AI, then it seems to have something really important to say to you. A recent paper by Tilmann Gneiting of the Universität Heidelberg puts the question very clearly: "Bob predicts a future observation based on a sample of size one. Alice can draw a sample of any size before issuing her prediction. How much better can she do than Bob?" it goes on to provide the surprising answer: "Perhaps surprisingly, under a large class of loss functions, which we refer to as the Cover-Hart family, the best Alice can do is to halve Bob’s risk. In this sense, half the information in an infinite sample is contained in a sample of size one." At this point you are probably thinking that there must be something very odd about the class of loss functions in the Cover-Hart family, but this doesn't provide an escape. As the paper proves, any metric and any negative definite kernel belong to the Cover-Hart family. This includes the squared error loss function - so estimation by least squares is included in the theorem. The paper gives a list of a range of loss functions that are contained within the Cover-Hart family: You can see that while the question remains of what constitutes the full Cover-Hart family, most of the measures of loss that we use in practice are included. The theorem not only applies to point estimators but to probabilistic predictions where the sample is used to construct a probability distribution for the estimate. In this case, defining the expected loss is more complicated but the results are very similar - a multi-sample estimate does no better than twice the expected loss of a single sample estimate. This has some interesting consequences. As the paper points out: Given that under many of the most prevalent loss functions used in practice, Alice, despite having an For example, this was observed in the Netflix contest, where predictive performance was measured in terms of the (root mean) squared error. "Taking a much broader perspective, the Cover-Hart inequality may contribute to our understanding of the empirical success not only of nearest neighbor techniques and their ramifications, but reasoning and learning by analogy in general." In other words, you can't get that much of an advantage no matter how clever your estimation procedure is and in many cases one look is sufficient to draw a conclusion. This is both depressing and encouraging.
More InformationOn the Cover-Hart Inequality: What's a Sample of Size One Worth?
Further ReadingIntroduction to Statistics – Your Access Pass to the Udacity Artificial Intelligence Track
Comments
or email your comment to: comments@i-programmer.info
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
|
|||
| Last Updated ( Monday, 25 June 2012 ) |