| Hunt for Missing Prime Numbers In the Cloud |
| Written by Sue Gee | |||
| Friday, 06 December 2013 | |||
|
Microsoft has launched the Prime Challenge, asking you to use cloud computing to find "lost primes". If this idea appeals to you can get a free trial subscription of Windows Azure to create and access virtual servers. People devote their lives to searching for prime numbers and there is a prize of $150,000 from the Electronic Frontier Foundation at stake for discovering the first prime with at least 100 million - and one of $250,000 for a prime with at least a billion digits. Earlier this year the 48th Mersenne prime was discovered, winning its discoverer, Curtis Cooper, a mathematician at the University of Central Missouri, a prize of $3,000 from the GIMPS project, the distributed computing project designed to hunt for Mersenne primes.
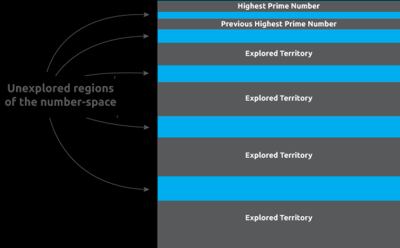
Microsoft's new challenge doesn't have any cash prizes and doesn't expect to break the record for the largest prime number, instead it wants to involve anyone with an enthusiasm for numbers to look for "the missing primes". The idea is to explore the areas in the number space that have previously been ignored in the expectation of finding "many of the lost primes". It is also hoped that the the challenge will also highlight which architectures and configurations of cloud computing resources work best for this kind of task. Announcing the challenge on the MSDN blog Planky explains: The identification of new prime numbers is increasingly challenging, but possible for anyone. Forty per cent of the numbers between one and ten are prime but, as we progress up the number line, they taper off and become sparser. But in reality, as we get much further up the number line, nobody really knows as nobody has ever searched for them all. In practice we probably do know quite a lot because the distribution of the primes, i.e. the number of primes less than n, has been known to be approximately given by n/ln n. With regard to "lost primes" the Prime Challenge website states:
The website goes on to explain that the algorithms used to search for very large prime numbers leave swathes fo the number space unexplored. It claims that there is"huge potential" for filling in gaps.
The challenge is open to teams and individuals and the first steps are to take out a free Windows Azure trial subscription which gives you a $200 allowance for 30 days and to sign up for the challenge. Next you need to build and configure the servers you need. There are videos explaining how to to accomplish these steps. Step 4 is where you start to discover prime numbers. You can do this with your own algorithm but the challenge has provided its own primality proving program, Primo developed by Marcel Martin. This video shows you how to use it and how to create text files with large decimal prime numbers in them ready to submit to the Prime Challenge Results Table.
Another video covers posing the new prime numbers you've discovered to the results table. The challenge runs until March 29th and we will have to wait and see it produces the modern day equivalent of the Sieve of Eratosthenes or comes up with a better algorithm than the Mersenne primes. At the moment the results list looks a little underwhelming as the seven so far listed are all tiny - we do know all the primes up to the first several million of them and well beyond ten digits. Will the search become more serious? You can't but help notice that it's all good publicity for Microsoft's Azure.
More InformationAnnouncing: The Prime Challenge Related Articles48th Mersenne Prime Discovered Prime Numbers And Primality Testing Reaching The Unreachable - Pi Squared And Catalan's Constant A Quantum Computer Finds Factors Solve The Riemann Hypothesis With A Quantum Computer
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Friday, 06 December 2013 ) |