| QScript A Quantum Computer In Your Browser |
| Written by Mike James | |||
| Thursday, 22 May 2014 | |||
|
Google's Chrome experiments are usually about impressive graphics, but this one takes us into the realm of quantum computing and this is about as esoteric as it gets. If you have ever wanted to try your hand at quantum algorithms, there is no longer an excuse.
Quantum Computing Playground is a browser-based quantum computer simulation. It makes heavy use of WebGL, and hence the GPU to run code written in Qscript, and shows you the results. It includes a range of examples that start off with some simple quantum gates and work their way up to Grover's and Shor's algorithm. Of course this isn't a real quantum computer - just some JavaScript running on standard hardware, unless the machine you use to browse the web happens to be a quantum computer. So there is no speedup in using the algorithms and it is a learning tool and perhaps a development tool in readiness for the day that quantum computing becomes commonplace. Who knows, you might be able to invent a new algorithm and have your name join those of Grover and Shor.
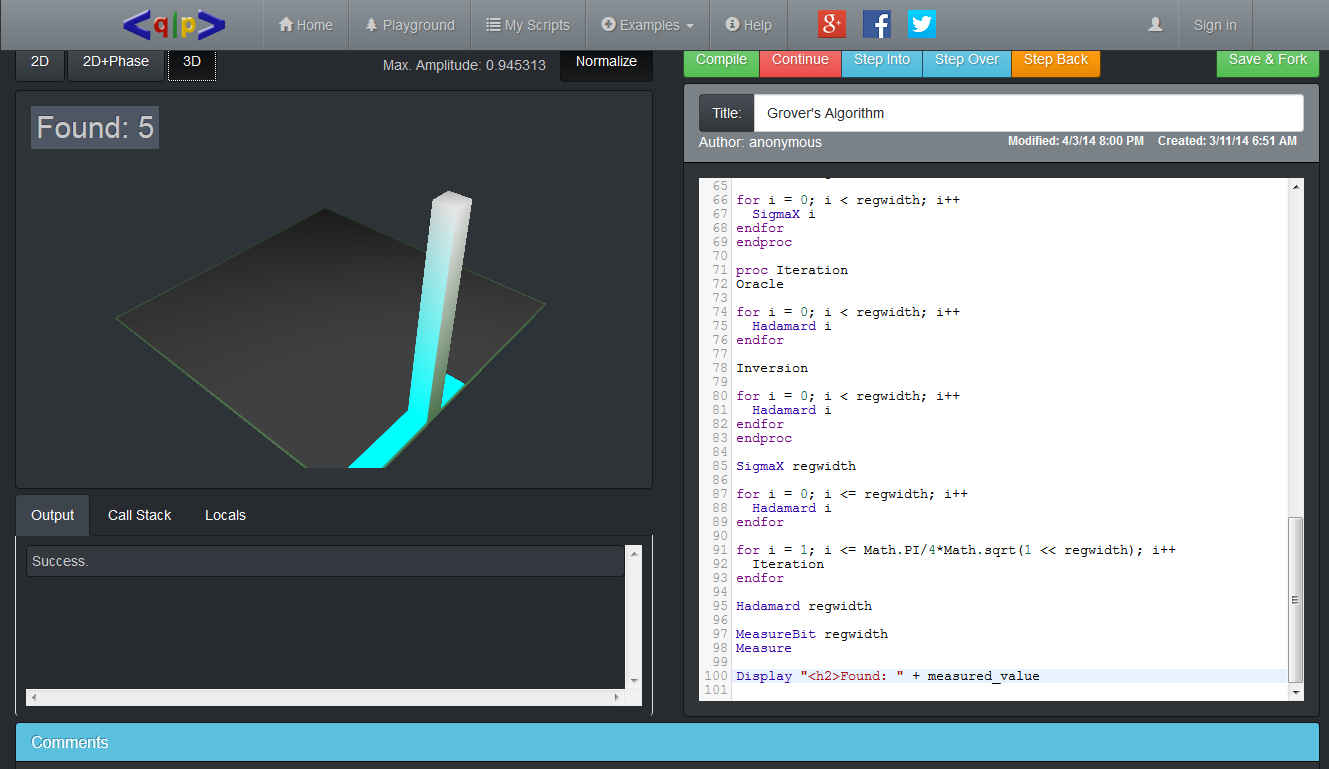
One of the problems with using it is that it doesn't provide a course in quantum computing or quantum principles and to make much sense of it you need to know something about quantum mechanics and have a rough idea if what quantum gates are all about. The documentation for the simulation is fairly non-existent and all you get to help you fathom how to use it are lots of examples. The biggest problem the beginner is going to have is working out what the output displays are actually displaying. If you set up a register with say two qubits - notice that the simulation only allow registers to be 6 to 22 qubits - then you have four quantum states available:
and the general state of the system is a superposition of these. These are the states that are plotted in the 2D display, not individual bits, so a register with 8 qubits has 256 states plotted in a 2D square. Each state is colored according to its phase and its amplitude is plotted as a height in the 3D plot. Quantum computation is performed by applying the state to a set of "gates" that transform the state. For example a Hadamard gate applied to bit n places that bit into a superposition of zero and one i.e. there is a 0.5 probability of measuring it as a zero or a one. So suppose we apply the Hadamard gate to the first bit of our two qubits that makes the first bit equally likely to be a zero or a one and so the overall state is an equal mix of |00> and |01> with the probability of all other states being zero. Once you have this basic idea you can learn about other quantum gates and how they can be put together to create useful computations, like Grover's search and Shor's factoring algorithms. What is interesting is that after we have been thinking about quantum computing for so long, only a few really useful algorithms are known - but Shor's alone is worth the effort of building a quantum computer. One of the more amusing things about quantum computation is that quantum gates are always reversible (they are unitary transformations) and as such any quantum algorithm is also reversible. This means that the debugger not only has a Step Into and a Step Over but a Step Back button. And yes, you can indeed reverse a quantum algorithm from its final state to its initial state, as long as you haven't made a measurement which is irreversible.
If only building a real quantum computer was just as easy. More InformationRelated ArticlesNobel Prize For Computer Chemists Solve The Riemann Hypothesis With A Quantum Computer Boson Sampling Tests Quantum Computing A Quantum Computer Finds Factors The Revolution In Evolutionary Game Theory - Prisoners Dilemma Solved? $100,000 Prize For Proving Quantum Computers Are Impossible
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Thursday, 22 May 2014 ) |