| Data Structures - Trees |
| Written by Mike James | ||||
| Sunday, 20 July 2025 | ||||
Page 1 of 3 Classic data structures produce classic tutorials. In this edition of Babbage's Bag we investigate the advanced ecology of trees - perfectly balanced trees, AVL trees and B-Trees. Trees and indexesThe tree is one of the most powerful of the advanced data structures and it often pops up in even more advanced subjects such as AI and compiler design. Surprisingly though, the tree is important in a much more basic application - namely the keeping of an efficient index.
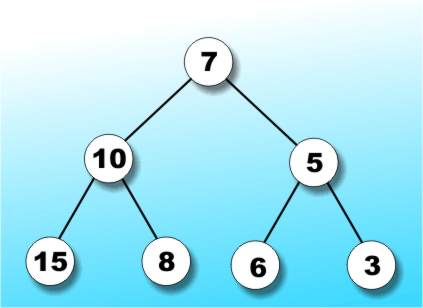
Whenever you use a database there is a 99% chance that an index is involved somewhere. The simplest type of index is a sorted listing of the key field. This provides a fast lookup because you can use a binary search to locate any item without having to look at each one in turn. The trouble with a simple ordered list only becomes apparent once you start adding new items and have to keep the list sorted - it can be done reasonably efficiently but it takes some advanced juggling. A more important defect in these days of networking and multi-user systems is related to the file locking properties of such an index. Basically if you want to share a linear index and allow more than one user to update it then you have to lock the entire index during each update. In other words a linear index isn't easy to share and this is where trees come in - I suppose you could say that trees are shareable. Tree ecologyA tree is a data structure consisting of nodes organised as a hierarchy - see Figure 1.
Figure 1: Some tree jargon
There is some obvious jargon that relates to trees and some not so obvious both are summarised in the glossary and selected examples are shown in Figure 1. I will try to avoid overly academic definitions or descriptions in what follows but if you need a quick definition of any term then look it up in the glossary. Binary treesA worthwhile simplification is to consider only binary trees. A binary tree is one in which each node has at most two descendants - a node can have just one but it can't have more than two. Clearly each node in a binary tree can have a left and/or a right descendant. The importance of a binary tree is that it can create a data structure that mimics a "yes/no" decision making process. For example, if you construct a binary tree to store numeric values such that each left sub-tree contains larger values and each right sub-tree contains smaller values then it is easy to search the tree for any particular value. The algorithm is simply a tree search equivalent of a binary search:
Of course if the loop terminates because it reaches a terminal node then the search value isn't in the tree, but the fine detail only obscures the basic principles. The next question is how the shape of the tree affects the efficiency of the search. We all have a tendency to imagine complete binary trees like the one in Figure 2a and in this case it isn't difficult to see that in the worst case a search would have to go down the to the full depth of the tree. If you are happy with maths you will know that if the tree in Figure 2a contains n items then its depth is log2 n and so at best a tree search is as fast as a binary search.
Figure 2a: The "perfect" binary tree .
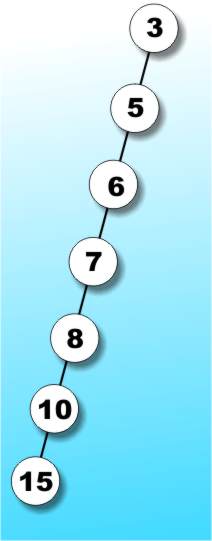
The worst possible performance is produced by a tree like that in Figure 2b. In this case all of the items are lined up on a single branch making a tree with a depth of n. The worst case search of such a tree would take n compares which is the same as searching an unsorted linear list. So depending on the shape of the tree search efficiency varies from a binary search of a sorted list to a linear search of an unsorted list. Clearly if it is going to be worth using a tree we have to ensure that it is going to be closer in shape to the tree in Figure 2a than that in 2b.
Figure 2b: This may be an extreme binary tree but it still IS a binary tree
All a question of balanceYou might at first think that the solution is always to order the nodes so that the search tree a perfect example of the complete tree in Figure 2a. The first problem is that not all trees have enough nodes to be complete. For example, a tree with a single node is complete but one with two nodes isn't and so on. It doesn't take a genius to work out that complete trees always have one less than a power of two nodes. With other numbers of nodes the best we can do is to ask that a tree's terminal nodes are as nearly as possible on the same level. You can think of this as trying to produce a tree with `branches' of as nearly the same length as possible. In practice it turns out to be possible always to arrange a tree so that the total number of nodes in each node's right and left sub-trees differ by one at most, see Figure 3.
Figure 3: A balanced tree
Such trees are called perfectly balanced trees because they are as in balance as it is possible to be for that number of nodes. If you have been following the argument it should be obvious that the search time is at a minimum for perfectly balanced trees. At this point it looks as though all the problems are solved. All we have to do is make sure that the tree is perfectly balanced and everything will be as efficient as it can be. Well this is true but it misses the point that ensuring that a tree is perfectly balanced isn't easy. If you have all of the data before you begin creating the tree then it is easy to construct a perfectly balanced tree but it is equally obvious that this task is equivalent to sorting the data and so we might as well just use a sorted list and binary search approach. The only time that a tree search is to be preferred is if the tree is built as data arrives because there is the possibility of building a well shaped search tree without sorting. <ASIN:0262033844> <ASIN:0071361286> <ASIN:3540435506> <ASIN:0521585198> |
||||
| Last Updated ( Sunday, 20 July 2025 ) |