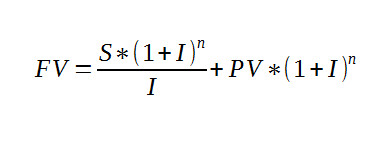| Cashflow Continued - Annuities |
| Written by Janet Swift | ||||
Page 1 of 3 We move on to annuities in the second of three chapters devoted to exploring the way in which interest rate affects cashflow. This chapter of Financial Functions with a Spreadsheet explores annuities. Financial Functions
Buy from AmazonSpreadsheets take the hard work out of calculations, but you still need to know how to do them. Financial Functions with a spreadsheet is all about understanding and reasoning, using a spreadsheet to do the actual calculation.
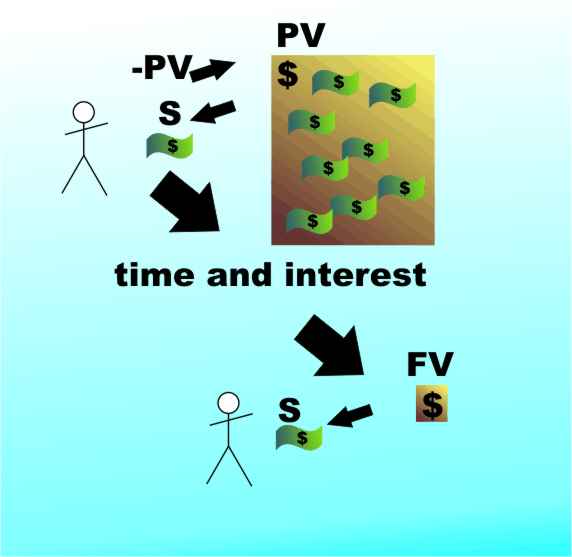
<ASIN:1871962013> <ASIN:B07S79ZVMQ> Although a savings plan (see Chapter 4) is just a special case of an annuity it has become common practice to apply the term to a particular type of investment where a lump sum is exchanged for a cash flow (contrast with a savings plan where a cash flow is exchanged for a lump sum). In the case of an annuity the cash flow reduces the principal but interest still acts to increase it. Annuities exploredIf the amount deposited is PV and the amount periodically withdrawn is S (which is positive as it represents cash flowing to you) then at the end of the first time period the balance stands at:
and at the end of the second:
and so on. Each month the balance earns I% interest and so increases by (1+I) but then S is removed from the account. In general after n time periods the balance stands at:
If you compare this situation with the savings plan you should notice that it is the same but with the regular payment positive (i.e. a cash inflow) and the initial deposit negative (i.e. a cash outflow).
An annuity - the deposit decreases as cash is withdrawn but interest still acts to increase it.
We already have a formula that gives the future value, i.e. the balance at time n, and it is just the formula used for the savings plan when there is an initial deposit PV :
and as long as we regard the cash flow as positive and the initial deposit as negative (i.e. money you paid out) then we don’t even have to change the sign of S in the formula. That is, the function: =FV(I,nper,S,PV) will calculate the Future Value FV of an annuity consisting of a regular payment of S, at I% for nper periods with a starting blance of PV. (Note that in Excel's terminology PMT is used for S and Rate for I.) In the case of an annuity PV is usually negative and the payment S is positive. For example, suppose we set up an annuity with a PV of -$1000, then at an interest rate of 10% per annum if we withdraw $100 each year the FV or balance at the end of one year is:
which gives $900. The reason is that the interest on $1000 is $100 making the balance at the end of the year $1100 and then we withdraw $200 reducing the balance to $ 900. The following year the balance will be:
which works out to $790 - i.e. plus $90 of interest and minus the $200 withdrawal and so on. |