| Investment Analysis |
| Written by Janet Swift | |||
Page 1 of 2 How is it possible to evaluate investments that generate irregular cashflows? We explore how NPV can be used to make investment decisions. This chapter of Financial Functions with a Spreadsheet explores what makes a good investment. Financial Functions
Buy from AmazonSpreadsheets take the hard work out of calculations, but you still need to know how to do them. Financial Functions with a spreadsheet is all about understanding and reasoning, using a spreadsheet to do the actual calculation.
<ASIN:1871962013> <ASIN:B07S79ZVMQ> In Chapter 7 the idea of the Net Present Value was introduced along with the associated quantity the Net Future Value. By looking at special cases it was demonstrated the the NPV was a reasonable measure of worth. However, this is a long way from being a complete or even reasonably plausible theory of how we should evaluate investments that generate irregular cashflows. In this chapter how NPV can be used to make investment decisions is described and justified. NPV and investmentLooking at the special case of the NPV of repayment loans, annuities and savings plans leads on to the consideration of more general investments. The idea of Net Present Value is perfectly applicable to cashflow and includes both positive and negative amounts over its entire lifetime. The negative flows represent the cost of the investment and the positive flows indicate the return on the investment. As long as we include all of the cash sums included in the investment then the NPV represents the value of the entire investment, i.e. the amount that would have to be invested at I% to produce the same worth as the whole cashflow. Notice that the NPV is does not represent the amount of money that you put into the investment - that is represented by the negative cashflows. We clearly need to investigate a little more closely what the NPV of the total cashflow of an investment actually means. The real question is what the negative quantities in the cashflow represent when reduced back to their present value. If the cashflow has an entry of -5000 at the end of the 3rd year, say, then what this means is that you are investing $5000. An alternative way of making this cash deposit at the end of the 3rd year is to deposit $5000/(1+I)^3 now, that is $3756.57 assuming 10% per annum, and allow it to grow to the required sum. In other words the present value of a negative sum represents the amount you would need to invest now to produce the you need to invest in the future. So in a cashflow containing both positive and negative values:
You can see that the NPV reduces both positive and negative cashflows to a fixed point in time - i.e. now. If the NPV is zero then this means that the amount that you invest is exactly equal to the amount that you receive back if you allow for the effect of the I% interest rate. If the NPV is positive then you have received more than you invested and if negative you have made a loss on the investment. This interpretation makes it very easy to formulate the basic rule of investment decision making. If you are considering an investment that leads to a cashflow then to decide if the investment is worthwhile compute its NPV and
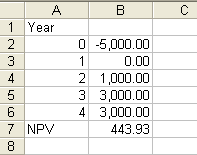
If the NPV is zero then you should be indifferent to the investment unless it has non-financial considerations that are not represented by the cashflow. If the NPV is negative then you are making a loss on the investment and you need a very good non-financial reason for accepting it! For example, if you are offered the chance to make a loan to a business start up of $5000. At the end of the first year you would receive nothing, in the second $1000 and in the third, and fourth years you would be repaid $3000 then, assuming an 8% ‘safe’ interest rate the NPV can be calculated as shown below.
The cashflow is entered into B2:B6 and the NPV is calculated by
in B7. Notice that as the first payment is at that start of the first year it is entered as Year 0 - this is a common convention concerning initial payments. The result of $443.93 indicates that there is a return over and above the ‘safe’ interest rate but how can we tell how good this return is? <ASIN:1871962013> <ASIN:B07S79ZVMQ> <ASIN:0190296380> <ASIN:1292214074> <ASIN:1119067510> <ASIN:078975584X>
|
 How good is the investment?
How good is the investment?