| Finding Solutions To Diophantine Equations By Smell |
| Written by Mike James | |||
| Thursday, 06 June 2013 | |||
|
Yes - smell. Diophantine equations are just polynomial equations that use nothing but integers for their coefficients and solutions. They are very hard to solve and often very important.
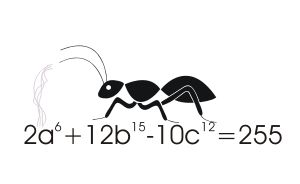
We know that there is no general solution - this was proved by Matiyasevich in 1970 who also showed that there was no solution to Hilbert's tenth problem. For example, find integers a,b and c that satisfy:
In this case a,b and c are just Pythagorean triples like 3, 4, 5, i.e. the sides of a right-angled triangle. Equally well known is the fact that the same equation, but with a power greater than two, doesn't have any solutions because this is Fermat's last theorem, as proved by Wiles in 1994. As the solution space consists of a discrete set of integers, it seems fairly obvious to try some AI search techniques to solve the general equation and people have tried things like the genetic algorithm, which represents potential solutions as genes and breeds new solutions by selecting breding pairs according to fitness. Now we have another approach from a team at Mumbai University - the Ant Colony Optimization algorithm. This works by allowing an "ant" to explore the solution space and leave a pheromone trail behind for others to follow. The idea is that the pheromone is deposited according to the goodness of the ant's location and it also evaporates to allow new areas of the space to be searched. What makes searching for a Diophantine solution different is that you might well have a set of integers that get close to a solution but the neighboring integer solutions over- or undershoot and so don't provide a solution. That are some seemingly good locations in the search space are in fact very bad. In this case the ants are set loose in the search space at random initial locations on an m dimensional grid - where m is the number of unknowns. The quality of the location is established by how close it comes to solving the equation. This is used to give the ant a quantity of pheromone which it distributes randomly among neighboring locations. Over time the pheromone concentration decreases using a law that emulates evaporation. Of course, ants move toward concentrations of pheromone. What is surprising about this procedure is that it not only works but it seems to work better than the genetic algorithm - sometimes by quite a lot.
So what is it about searching for integer solutions that makes Ant Colony Optimization work? Possibly it is the simple fact that near a solution there are a lot of very good approximate solutions - consider changing one of the m variables in a solution by 1. This makes the problem more suitable for this sort of discrete "hill climbing" method. Whatever the reason, I doubt many mathematicians will think that "smelling" a solution in this sense has much beauty or elegance about it. More InformationFinding Numerical Solutions of Diophantine Equations using Ant Colony Optimization Related ArticlesMSDN Magazine April 2012 - C++AMP, Kinect and Bacteria Ants AI Challenge Winner Announced
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Saturday, 19 March 2016 ) |