| Quadtrees and Octrees |
| Written by Mike James | |||
| Thursday, 09 August 2018 | |||
Page 1 of 2 If you do any advanced work in graphics, sooner or later you will meet the Quadtree or its 3D relation, the Octree. For this reason alone they are worth knowing about, but they are also something you should have in your armory of data structures.
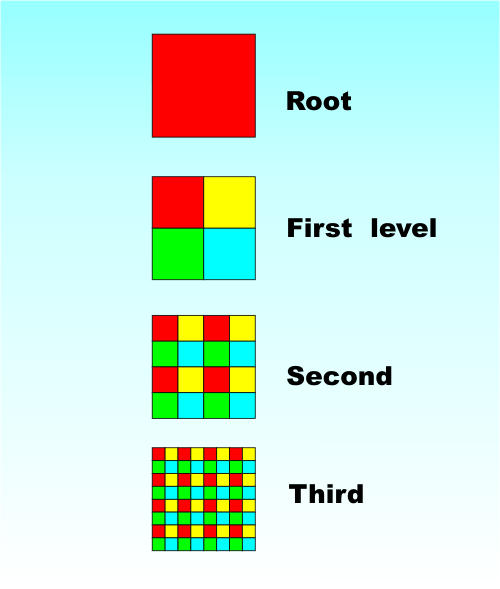
The Quadtree and its three-dimensional brother the Octree are two fundamental data types. They have lots of applications but the reason I am writing about them is that I've been working on a number of implementations of graphics algorithms, in particular custom color reduction, that need both data structures. However, the theory of these two data structures is well worth knowing even if color reduction isn’t something that interests you. Also, for reasons that I’m not at all sure of, both the quadtree and the octree are often ignored or forgotten when they could be really useful. The QuadtreeIt makes sense to start with the quadtree because it is simpler to explain – and draw! A quadtree derives from the idea of dividing a square area into smaller squares. This connection with squares and refinement also determines where it tends to be useful, i.e. in 2D search or optimization algorithms. Start with a unit square as the root of the tree. Now divide the square into four smaller squares. Each of the new smaller squares is a child node of the root. The next step is to repeat the process on the small squares generating four more sub-squares and hence four children at the next level of the tree for each of them.
As you move down the quadtree each square is divided into four smaller squares.
At first it can be difficult to see the tree for the squares but the diagrams should help.
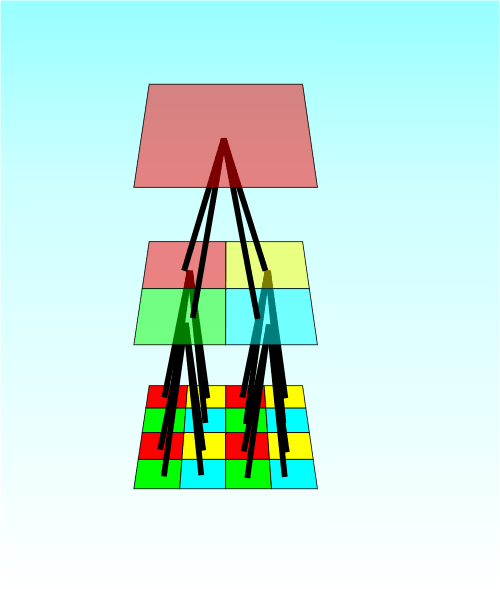
You can see how the tree idea fits into the picture a little better by drawing lines showing the children of each node. If you concentrate on the black lines you can see that they form a branching tree structure with four branches at each level.
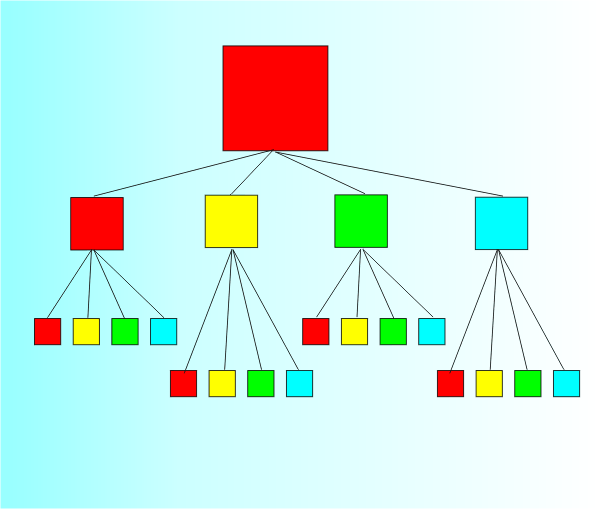
We can make the view of the tree more abstract and closer to the data structure we use to represent it by flattening the tree part of the diagram into a 2D tree diagram.
You can now see that a quadtree isn't really very special as a data structure - its just a tree where each node has four child nodes. The key idea however is that each child node represents a subdivision of the square that its parent node represents. Most of the work in implementing a quadtree goes into representing and implementing the division of the geometry rather than in building a sophisticated data structure. There are other potential complications that you can encounter in practice. For example, it is usually the case that a quadtree is built up dynamically as the data becomes available. In this case the division of a square at one level may become necessary before some or any of the others have been divided. The result is an unbalanced quadtree the covers some areas more finely than others. This might seem like a complication but it has big advantages in that the 2D area is covered only as finely as is necessary. Fast sortingOK so now you understand the quadtree – what use is it? The answer is that the different levels of the tree provide different resolutions of detail and this can be useful in many different ways. For example, if you have a two-dimensional data point, x,y, then this will fall in exactly one node at each level of the tree. You can use this fact to perform a fast search of a data set. First sort the data into a quadtree and then when you want to see if a particular data value x,y is present you simply move down the tree via the correct node at each level until you reach the bottom and find the point or discover it isn’t present. This is the two-dimensional equivalent of the binary search algorithm used to search a one-dimensional list. Such algorithms have some surprising applications for example if you want to make Conway's Game of Life (The Meaning of Life ) go faster then use a quadtree. You can also use the same technique as a method of data compression. For example if you divide up a map using a quadtree then you can give every house a compressed location according to the right or left branches needed to reach it. For example, 2312 would mean the house that you find when you start at the root, go down branch 2, then 3 then 1 and finally 2. |
|||
| Last Updated ( Thursday, 09 August 2018 ) |
 The most abstract view emphasises the tree, but remember where the squares come from.
The most abstract view emphasises the tree, but remember where the squares come from.