| Public Key Encryption |
| Written by Mike James | ||||||
| Sunday, 18 August 2024 | ||||||
Page 2 of 2
RSATo create the key you first start out by picking two large prime numbers. Finding large primes isn’t too difficult but to keep the arithmetic simple let's pick small primes for our example: p=3 and q=11. The product of 3 and 11 is 33 and this is the first part of our key
As well as the product of the primes we also use the product of one less than each of them, i.e.
as another part of a key. Next we need another prime, d, in the interval [max(p,q)+1,n-1]. In our case the interval is [12,32] and we can pick d=13 as a suitable prime. That is
This all sounds complicated but we are almost done. We just need one more number to complete the keys. We need a value e such that
If you need a refresher on the Mod function then see Mod function. But put as simply as possible the n Mod m is the remainder when you divide n by m. Another way of think of this is to "clock arithmetic" and allow values to wrap round at m. In this particular case we need to find a number e, an integer, that when you multiply by d and allow the result to wrap round at m you get the result 1. For example, 4*2 Mod 7 = 8 Mod 7 = 1 Mod 7
Notice that
looks like e*d=1 if you forget the Mod part. You can see that in this case e is just 1/d that is e is just the inverse of d. If you put the Mod function back in you can see that e is the inverse of d Mod m. There is a fairly simple well-known algorithm for working out modular inverses, as e in the formula above is called, so in practice you don't have to guess or spend hours working it out from scratch. In our case the problem is to find an e such that
and you can verify that e=17 gives the required result. Now we have a lot of numbers and it is worth summarizing what they all are:
The two numbers e and n can be published as the public key (e,n) and d and m are keep secret as the private key (d,m). If you want to send a coded message all you have to do is use:
where M is the value that corresponds to the data C is the encrypted value and Me means raise M to the power of e. Notice that to encode the value we use both parts of the public key e and n. For example, the letter “E” is the fifth letter i.e. M=5 and our public key is (17,33) therefore the encrypted character is:
So to transmit an encrypted “E” we send a “14”. Cracking the Code?This might not seem very secure but consider the problem of someone wanting to crack the code. They know the public key (e,n) and they know the code word – 14 and to recover the message they have to solve:
That is, they have to find M such that it gives 14 when raised to the 17th power mod 33. This turns out to be a very difficult problem – unless you happen to know d. In fact any solution to the problem is equivalent to knowing d. If you do know d then you can write down the solution at once:
which is of course the number we first thought of as a letter “E”. Now suppose that you don’t know d but want to find it to crack the code. This should be easy as we all know that
and this is reasonably easy to solve, but wait, we don’t know m! If you recall the private key is (d,m) and all we know is (e,n). However surely knowing n we can work out m because n is just p*q and m is just (p-1)*(q-1). So all we have to do is find the prime factors of n, use these to construct m and finally solve to find d and again - all is lost! Finding factorsThis may sound complicated but to gain the information that has been encrypted it is worth it and after all factoring a number is easy – wrong. Factoring a small number is easy. For example, in our case we can find the prime factors of 33 by trial and error. All we have to do is test to see if each prime smaller than 33 divides 33. In fact most of us are so good at arithmetic that we immediately notice that 33=3*11 and so p=3 and q=11. From this we can recover the first part of the private key m=(p-1)*(q-1)=20 and from this we can find d as the solution to
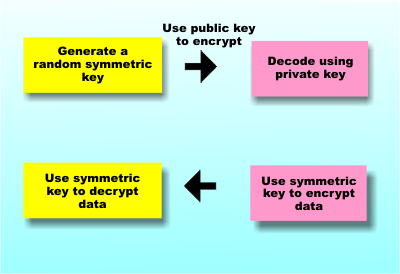
which is very easy. So the security of the entire scheme depends on how hard it is to factor a number. To see just how hard, try factoring 53357, which I promise is the product of two primes. If you manage that try 62773913 and so on. Public key cryptography generally uses very big primes which makes the task of recovering them very, very difficult. So it all works and it is all secure – unless you know how to factor numbers really fast! Currently this is still a problem that is difficult although mathematicians are finding short cuts public key cryptography seems to be secure and quantum computing promises to solve the problem in just one weird quantum step - A Quantum Computer Finds Factors Finally one last complication because public key cryptography is computationally intensive it generally isn't used to encode lots of data. Instead it is used to exchange keys which are then used in symmetric encryption methods. In this sense public key cryptography is the answer to the key exchange problem we mentioned earlier. That is you use public key cryptography to start the transaction and then shift to a good old symmetric key method once the keys have been exchanged. What this means however is that no matter how good your symmetric key encryption is if a quantum computer can factor large numbers then the key exchange is compromised. If the key exchange is compromised then the key for the symmetric key algorithm can be found. The symmetric key algorithm is only as secure as the public key cryptography is.
Public key encryption is really used to send keys which are then used to send the real data So quantum computers can crack all of the codes? Not necessarily even if they can be built. The reason is that we are moving to Quantum resistant codes. The NIST recently announced the standardization of three post-quantum cryptographic encryption schemes. If we all switch to one or more of these proposed schemes it could be that the only thing a quantum computer can be used to break are old codes - but this still might be worth the effort! Related ArticlesA Quantum Computer Finds Factors How Error Correcting Codes Work Introduction to Cryptography with Open-Source Software Prime numbers and primality testing
Comments
or email your comment to: comments@i-programmer.info To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin. 
<ASIN:0849308224> <ASIN:0521008905> |
||||||
| Last Updated ( Sunday, 18 August 2024 ) |
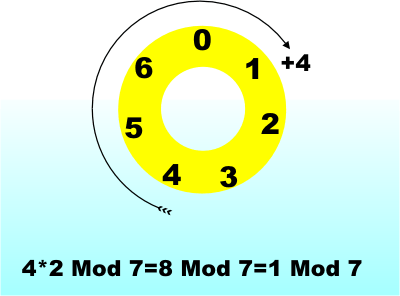.Modular arithmetic in action
