| Neural Turing Machines Learn Their Algorithms |
| Written by Mike James | |||
| Wednesday, 05 November 2014 | |||
|
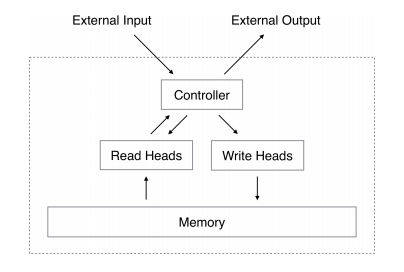
Another breakthrough at Google DeepMind? A neural network form of the Turing machine architecture is proposed and demonstrated, and it does seem to learn its algorithms. One of the problems with neural networks is that we know they are powerful in theory, but in practice training them and getting them to learn what we want turns out to be difficult. For example, a feedforward network with three layers can learn any function and a recurrent neural network RNN is Turing complete and so can compute anything that can be computed. What we need are some rules and ideas for giving the networks more structure so that they live up to their promise. After all, the human brain isn't just a randomly connected set of neurons it has functional units that do particular jobs. The Neural Turing Machine NTM is modeled on the standard Turing machine design - but using neural networks to implement the functional units. A standard Turing machine consists of a control unit and a tape. The control unit is a finite state machine that can read and write the tape. As it reads symbols it changes state and then writes a symbol. This is a model of what computation is and, while it can in theory compute anything that can be computed, it isn't a practical machine. The neural Turing machine also has a control unit and a memory that is a little more powerful than the Turing machine's simple tape. The control unit can either be a simple feedforward network or a recurrent neural network. The memory takes the form of a matrix of values that is updated in a more gradual manner than a standard digital memory. A write operation consists of an erase operation, which is like a multiplication by 1-w, i.e. it reduces what is stored by a factor of w, and an add operation which then adds w to the location. You can see that the memory can operate in such a way that memories fade and are slowly replaced by new ones. If you know about Hopfield networks this will sound familiar, and indeed the memory is a modified content addressable memory. So far this just sounds like an attempt to make a Turing machine from neural network components, but there is something very different about this form of machine. All of the components work with continuous values and the entire machine is differentiable. That is, you can quantify the change in the output that any change in the inputs brings about. This means that you can use standard back propagation to train the neural Turing machine and this is a very big difference.
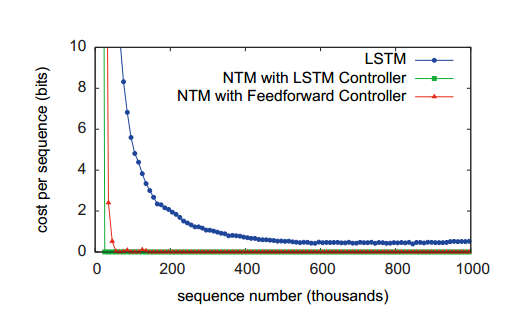
Of course, the fact that you can train a machine doesn't mean that it will learn anything well or particularly useful. So the team of Alex Graves, Greg Wayne and Ivo Danihelka turned their theory into a program and trained it on some suitable data. The first was to get the machine to copy an input sequence. Random binary sequences were presented and the target that the machine was trained to produce was just the sequence again. This sounds trivial, but you have to keep in mind that the sequences were variable in length and when tested the machine wouldn't have seen the testing sequences. In other words to perform, well it had to learn an algorithm that it had to store and reproduce any sequence presented to it. The results are very convincing. The neural Turing machine learned very rapidly compared to a standard LSTM network that would usually be used in this sort of task:
Notice that two versions of the neural Turinig machine were tried; one with an LSTM as its controller and one with a standard feedforward network. You can see from the error curves that the both achieved results that are of a different nature to the LSTM on its own. When the learned structure of the machine was examined it was discovered that the sequence of operations corresponded to the algorithm:
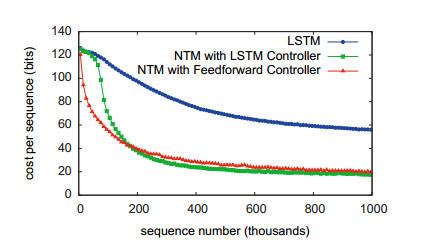
To quote from the paper: "This is essentially how a human programmer would perform the same task in a low-level programming language. In terms of data structures, we could say that NTM has learned how to create and iterate through arrays." The next task was to learn to copy sequences a given number of times. The algorithm it had to learn was essentially the previous one inside a for loop. This is achieved perfectly, but with more training. Next it learned a task that required it to perform associated recall and then one that required learning an n-gram model. The final task is perhaps the most impressive - learning to sort data. The NTM was trained on a set of data that consisted of a binary vector with a scalar priority rating. The target was the same vectors sorted into order according to the priority rating. The NTM learned to do this using either type of controller, but the traditional LSTM didn't really manage it: What algorithm was learned? The researchers hoped that the NTM would invent a binary heap sort, but in fact it seemed to have invented a hash table. The vectors were stored in memory locations controlled by the priority and then read out in priority order to give a sorted list. What does all of this mean for AI? We have a new neural network architecture which seems to be capable of solving problems in a way that can be interpreted as creating an algorithm. The connection with a Turing machine is probably not important and we shouldn't read very much into it. The NTM is perhaps better regarded as an architecture which successfully combines a processing network with a memory in such a way that they can both be trained. If this really works it would be worth seeing what it makes of today's difficult problems - robot bipedal walking, language understanding and plasma containment, for example. More InformationRelated ArticlesSynaptic - Advanced Neural Nets In JavaScript Google's Neural Networks See Even Better The Flaw Lurking In Every Deep Neural Net Google's Deep Learning AI Knows Where You Live And Can Crack CAPTCHA Google Uses AI to Find Where You Live Google Explains How AI Photo Search Works Google Has Another Machine Vision Breakthrough?
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Wednesday, 05 November 2014 ) |