| DeepMind Solves Quantum Chemistry |
| Written by Lucy Black | |||
| Sunday, 08 September 2019 | |||
|
The best known applications of neural networks are in AI - vision, speech and game playing - but they have serious applications in science and engineering. Google's DeepMind has trained a neural network to solve Schrodinger's equation and this is potentially big news. Any physicist will tell you that chemistry is just a branch of applied physics. Well to be honest they will tell you that just about any other subject is a branch of applied physics, but in the case of chemistry they are closer to being right. Chemical reactions are basically all about electrons and how they orbit atoms and molecules. The differences in energies control how things react and the orbits of electrons in molecules determine the shape, and hence the properties, of the substance. In principle then, chemistry is easy. All you have to do is write down the Schrodinger equation for the reactants and solve it. In practice, this isn't possible because multi-body Schrodinger equations are very difficult to solve. In fact, the only atom we can solve exactly is the Hydrogen atom with one proton and one electron. All other atoms are solved by approximations called perturbation techniques. As for molecules - well we really don't get off the starting blocks and quantum chemists have spent decades trying to perfect approximations that are fast to compute and give accurate results. While progress has been impressive, many practical calculations are still out of reach and in these situations chemistry reverts to guesswork and intuition. Neural networks can be thought of as function approximators. That is, you give a neural network a function to learn and it will. You present the inputs, the x, and then train it to produce f(x), where x in this case stands in for a lot of different variables. The idea is that it learns to produce the known values of f(x), i.e. the ones you give it as the training set, but it also manages to produce good results when you give it an x it has never seen. We usually say that neural networks generalize well. More accurately we hope that they do because this means that when they have been trained to recognize a cat they can still recognize a different cat that wasn't in the training set. In AI applications it seems reasonable that somehow the network has extracted the essence of "cat" and can now generalize. In more abstract function approximations, it is more difficult to imagine the "cat" in the equations. In this case the network does seem to have extracted the cat from Schrodinger's equation - and I leave you to make your own jokes...
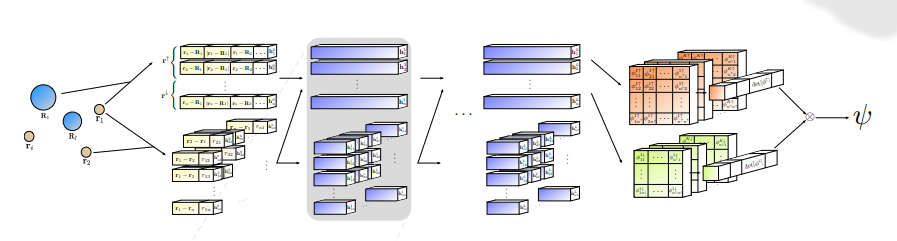
What exactly the neural network does is find an approximate multi-electron wave function that satisfies Fermi-Dirac statistics, i.e. the wave function is antisymmetric. All that is needed are the initial electron configurations - how many etc - and the neural network will then output the wave function for any configuration. The network was trained to find the approximation to the ground state wave function by minimizing its energy state. The ground state is by definition the state with the lowest energy and the network varied the parameters until it reached a minimum. As the paper states: "Here we introduce a novel deep learning architecture, the Fermionic Neural Network, as a powerful wavefunction Ansatz for many-electron systems. The Fermionic Neural Network is able to achieve accuracy beyond other variational Monte Carlo Ansatz on a variety of atoms and small molecules. Using no data other than atomic positions and charges, we predict the dissociation curves of the nitrogen molecule and hydrogen chain, two challenging strongly-correlated systems, to significantly higher accuracy than the coupled cluster method, widely considered the gold standard for quantum chemistry." Nitrogen is a difficult molecule because of the existence of a triple bond that has to be broken. "For the Fermi Net, all code was implemented in TensorFlow, and each experiment was run in parallel on 8 V100 GPUs. With a smaller batch size we were able to train on a single GPU but convergence was significantly slower. For instance, ethene converged after just 2 days of training with 8 GPUs, while several weeks were required on a single GPU" There are roughly 70,000 parameters in the network and the real question is what generalization is occurring here? The network is trained just once and after this it seems to be capable of finding approximate wave functions that give good results for the predicted properties. "Importantly, one network architecture with one set of training parameters has been able to attain high accuracy on every system examined." How much can we trust a neural network that we just don't understand? This is the one potential misgiving of relying on these findings. However they are probably too good to just ignore because we don't understand the way the network constructs its optimum functions. As the paper concludes: "This has the potential to bring to quantum chemistry the same rapid progress that deep learning has enabled in numerous fields of artificial intelligence."
More InformationAb-Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks Related ArticlesAll You Wanted To Know About AI From DeepMind Nobel Prize For Computer Chemists Software Bypasses Drug Patents To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Sunday, 08 September 2019 ) |