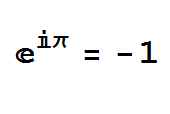| Pi Day Of The Century |
| Written by Mike James | |||
| Saturday, 14 March 2015 | |||
|
Pi day is the 14th of March every year because 3.14 are the first three digits of Pi but this year the date is 3/14/15 and these are the first five digits of Pi - 3.1415. This only happens once per century so let's celebrate! If you really want to take it to extremes then you could begin your celebration on 3/14/15 at 9:26 i.e. 3.1415926. I suppose, you could even carry it on to even smaller time divisions and even pick an exact moment of time that was Pi to every decimal place. Yes, in this sense there is exact Pi moment. Pi is a very strange number.
Non-math types, and even some fanciful math types tends to latch onto the use of the words "irrational" and "transcendental" to make Pi special but the truth is that there are more irrational and transcendental numbers than any other type. In fact there are an uncountable infinity of them. What makes Pi special is that it captures a property of space. It only has the value we give it in a flat Euclidean space. In a curved space Pi has a different value. Pi measures the way that the area or volume in general scales as you make a shape bigger or smaller. When Pi turns up in a formula it generally has something to do with the way something scales as you change its size, even if this isn't obvious from the way things are described. There is a second aspect of Pi that makes it turn up everywhere. As the circumference of a unit circle is exactly 2Pi long you can use it to measure angle. Start at a point on the circle and move round - measure how far you have gone and you have a measure of angle that is in terms of fractions of 2Pi. If you go a distance of Pi/2 then you have rotated by 90 degrees, Pi is 180 degrees (half way round) and of course 2Pi is a full rotation. This is radian measure of rotation and it is another reason why Pi occurs in many formulas. For example, the most beautiful equation in math is generally said to be:
and it is all because a rotation by Pi is 180 degrees. When it comes to computation Pi is very special. Most irrational transcendental numbers are non-computable, which roughly means that there isn't an algorithm that gives their decimal expansion or any representation. Pi is irrational and transcendental and yet it seems very computable. There are lots of formulas for it and there are even formulas that will give you its nth digit without having to compute all of the digits leading up to the nth digit. This is remarkable. And yet this most computable number appears to be random when you look at its decimal expansion. It is even conjectured that it is a normal number, which means that if you specify a sequence of digits then it will occur somewhere in the decimal expansion of Pi. Which means that somewhere within Pi are the complete works of Shakespeare, your birth date and phone number. This has given rise to programs that will find your birthday in the expansion of Pi - a popular pastime on Pi day, as is eating pie...
Have a look at some of our previous Pi Day articles for more fun facts.
More Informationhttp://en.wikipedia.org/wiki/Pi_day I Prefer Pi: Background for Big Pi Day (3/14/15) MathHappening: Pi Day of the Century! Related ArticlesThe Life Of Pi - Yes It's Pi Day Celebrate Pi Day It Contains All Human Knowledge Normal Numbers - A Video In Rhyme Reaching The Unreachable - Pi Squared And Catalan's Constant 60 trillionth binary digit of pi-squared calculated Yahoo! Gets to the 2 Quadrillionth bit of Pi - it's zero
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Sunday, 14 March 2021 ) |