| Jigsaw Puzzles and The MacMahon Squares |
| Written by Joe Celko |
|
Another puzzle featuring Joe Celko's characterful pair, Melvin Frammis, an experienced developer at International Storm Door & Software, and his junior programmer sidekick, Bugsy Cottman. This classic puzzle looks deceptively simple but can you produce some beautiful code to solve it? UPDATE: Reader Frans Fasse has come up with an Exact Cover Solver in C++.
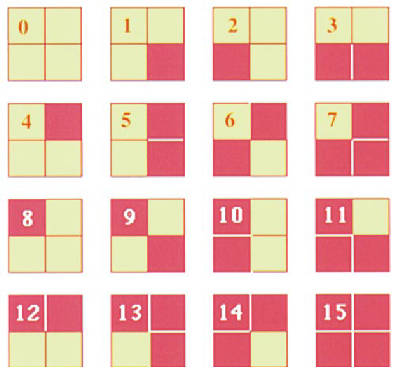
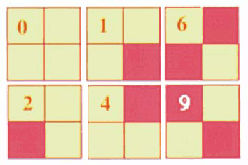
“I hate jigsaw puzzles. My first wife was a jigsaw puzzle junkie and she covered every table top with them.” grumbled Larry Smead as he sat down at the break table at International Storm Door & Software. “I am of the opinion that the jigsaw puzzle designers should have made all of the pieces uniform in color, shape and size, to make it easier and faster to assemble the final product. Why waste time with something which you have to fold up and put back in a box, anyway?” “What brought that on?” asked Bugsy Cottman looking up from his coffee and newspaper. Larry was always a little weird even for a developer and prone a mix of ADD and OCD. “Sorry, me and the ex-wife are fighting again. I saw you doing a picture jumble puzzle and it triggered me. Those jumble guys got it right.” apologized Larry. Bugsy decided not to ask which ex-wife. Melvin Frammis walked over to the table with his drink and candy bar. “Larry, if you want to play around with a jigsaw puzzle like that, talk to Jones in maintenance. He has a box of square carpet floor tiles that he needs to lay in the small conferences rooms on the fourth floor.” said Melvin. “What is so hard about laying square tiles?” “Glad you asked! Each set has 16 tiles. Each tile is divided into four quarters. Each quarter is colored either red or white. The set has all possible arrangements of the colors and assigned a code number to them on the back. You cannot rotate the tiles; they have grooved locking edges.” said Melvin as he pulled out a flyer from his jacket. “Someone already glued tile #0, the all-white one, in the front corner of each room.” “I think I get it.” said Larry. “Each tile is a binary number, with white as zero and red as one! I get four-sided domino. Clever.” “The tongue & grooves are such that tiles cannot rotate and have to match on their edges, like a jigsaw puzzle. Think you can write a program to give Jones different tilings that will cover the rooms? The rooms are square with four tiles to a side.” Larry's OCD kicked in and he wandered off talking to himself and drawing pictures on a paper napkin. “Thanks for distracting him, Mel", said Bugsy. “Have ever been cornered when he gets hung up on his ex-wife?” “Which one? Crazy Cat Lady? Crossword puzzle girl? Super Vegan? Larry does not marry well.” ChallengeYour problem, dear reader, is to find all of the tilings with the all-white tile in the upper left corner. For example, you can start to put tiles the together like this:
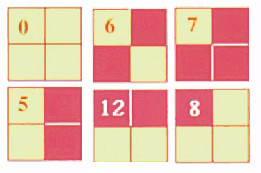
but not like this: : You can see that it is an interesting combinatorial problem to place all of the tiles together in a grid so that they obey the matching edges rule. It isn't even obvious that it can be done at all. This puzzle is a version of MacMahon squares, after their inventor, Percy Alexander MacMahon (1854-1929), an English mathematician and author of Combinatory Analysis (1915, reprinted in several editions) and New mathematical pastimes (1922, reprinted 2012). See the side panel for these and for other books that include it.. You'll find a good explanation of MacMahon 3-Color Squares on this blogspot and the entry in The Encyclopedia of Science also introduces 4-color triangles. If you want to go even futther see MacMahon's Coloured Cubes For bonus points, you can try to solve the Multimatch puzzle from from Kadon Enterprises http://www.gamepuzzles.com/edgemtch.htm#M1.
These square dominoes use all possible combinations of three colors on the edges of the dominoes, to give a set of 24 pieces. Kadon Enterprises deserves a shameless plug for their fine puzzles and games and I would recommend getting their catalog. Update:Reader Frans Faase wrote a program to find the solutions. "My first idea was to convert the problem to an Exact Cover problem. However, it did not find any solutions. This made me think about a program that could find the best almost solution. When I finished the program, it found 46 solutions. After some debugging, I found a bug in the algorithm to generate an Exact Cover and my Exact Cover solver found the 46 solutions with a second. I combined both algorithm in one program, written in C++." You can see all 46 solutions on his website which is well worth a visit for other topics. If you would like to send in a solutions to this puzzle email editor@i-programmer.info. Or use the comments below to discuss how to approach it.
Joe Celko is best known as the database expert who writes books on SQL, data and databases. But before that, he was an honest developer obsessed with finding good algorithms and clean code.
More puzzles tackled by Melvin, Bugsy & coVertex Coverings And The Cool Kids Problem Sharpen your Coding Skills - Elevator Puzzle Related articlesUnshuffling A Square Is NP-Complete
Comments
or email your comment to: comments@i-programmer.info
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
<ASIN:0821828320> <ASIN:0486495868> <ASIN:1418182451> <ASIN:111559690X> <ASIN:0199601399> <ASIN:B009YQK83U> <ASIN: 0140207139> <ASIN:0810907658> |