| Robot cars - provably uncrashable? |
| Written by Mike James |
| Wednesday, 13 July 2011 |
|
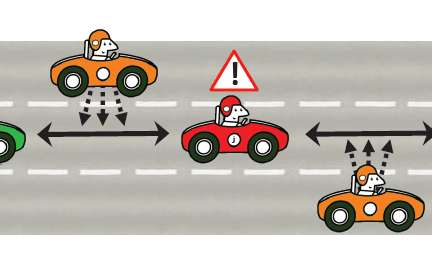
Robot cars are no longer the stuff of science fiction and in the future only a minority of cars will be driven by humans. But can we be sure what will happen when all cars are driven autonomously? One robot car might be safe but this doesn't mean that a road system full of them is. And then there is the small matter of the autonomous car hacker. They may not exist yet but they will. There is no doubt that the day of the self-drive or robot car isn't far off. Various states and countries have made self-driving cars legal and Google, Uber and most car companies are allowing cars to control themselves with the help of a human overseer, see Google drives a car. There are even intermediate solutions being tried out by mainstream car companies such as VW with its autopilot which takes the wheel while being monitored by the driver. In the future it will be, if not actually illegal, extremely bad taste to drive. The car's systems will be so good that even wanting to drive will be taken as a statement that you have no respect for your life and worse still no respect for others. Of course all of this depends on one single assumption that self drive cars will be safer and by a very obvious and noticeable margin. The problem with this is that we all know how buggy and unreliable the average piece of software is. Even automotive software, created to be more reliable than the average, has come under suspicion on occasion. So how can we prove that the software actually works?Using formal methodsWhen questions like this are asked the attention generally shifts to "formal methods". The rough idea is that programming is like mathematics and if you can convert it to be even more like math then you can prove that a program is correct in much the same way that you can prove a theorem is true. A team at Carnegie Mellon University has applied formal methods to adaptive cruise control and proved that cars using it cannot crash - as long as the road is straight! This has been reported as CMU having proved that self-drive cars are safe or something similar. Even the most restrained reporting is saying things like: Carnegie Mellon Methods Keep Bugs Out Of Software For Self-Driving Cars. This is bound to provide a level of good feeling toward a self-drive car. After all a human driver isn't provably crash proof in fact they are demonstrably crash prone! But it all depends what you mean by "provable". The problem of specifying the system formally is very difficult as it is a mixture of dynamics and logic - but this is the area that the researchers at CMU have extended formal methods into. Even so the situation to be modeled is very complex so the researchers started from a two-car situation and created a formal specification that included a differential equation modeling the dynamics. The model also assumes that the first car will accelerate and decelerate randomly. They then go on to prove that if the car behind is at a safe distance when the model is started they will never collide. Next they moved on to consider n cars in a single lane and proved that if these started off at a safe distance then there would be no collisions. However, the ordering of the cars is assumed to be fixed i.e. no overtaking. The next step is to allow cars to cut and move out of lanes. This is done by simply making cars appear and disappear in the lane. Not realistic but again provably safe. Finally we reach the pinnacle of reality - a multi-lane highway with cars that change lanes. The change of lane maneuver is modeled by making a car exist in both lanes for a time and then fading its existence out on the original lane This is far from realistic but again if everything starts from a safe configuration it remains safe and no collisions can occur.
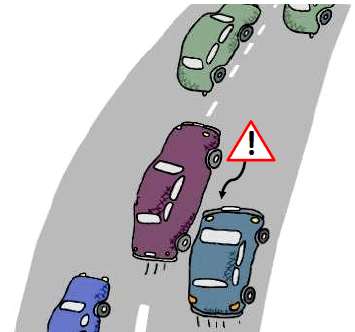
Collective behaviourBy now you should be able to see that the restriction to a straight road isn't the only problem with the proof of safety. While this sort of work is needed and worthy, its meaning has a tendency to be over played. It is closer to the proof that the solutions to a particular differential equation are stable - if the differential equation applies in a real situation and if it does what the effect of noise and imperfections has on the situation is another issue. What the work does draw attention to is the need to model the collective behaviour of self drive cars. It is possible that while one car might be safe enough driving on empty roads, or driving on roads that have cars driven by humans even, when road containing lots of robot cars it is another matter. Have you noticed the phenomenon where a fast road comes to an almost stop and yet when you get further on there is no obstruction or problem? This is supposed to be due to the increased braking effect. A driver at the front of a line slows for some reason, the next driver slows even more and so on until you reach the driver who slows so much that they come to a halt. Now think about robot drivers. It is interesting to ask if a line of robot drivers with faster response times and less sloppy driving might well have other similar modes of group behaviour. Could a line of robot cars oscillate for example? Could that oscillation get out of control? Could the effect of the sequential slowing for a corner cause a backup to a halt further up the road? Clearly it isn't sufficient to consider only straight roads when examining collective behaviour. There seem to be three situations that need analysis:
And the probably safety of any one doesn't say very much about the safety of the others.
Cascade failureProgrammers are by now very used to the fact that parallel programs have problems that go beyond what you get in simple sequential programs. They exhibit race conditions and deadlock for example. You can also get more complex behaviour out of parallel systems that are built of simple units than you might expect. For example cellular automata's follow simple rules but create amazingly complicated patterns. It should be obvious from this that it isn't enough to test a single robot car or prove that a single robot car is safe because it could be that when you put robot cars together you get new emergent behavior. Simple linear analysis may not be enough to predict the behaviour and non-linearities caused by ageing and the effects of noise might be significant. The point is that while you can get so far testing a robot car on roads that contains nothing but cars driven by slow to react and fallible humans the real test only starts when the same car is driven on roads full of similarly programmed cars with lightening reaction times and deterministic actions. It might be that the AI and the response times can out manoeuvre any human driver and deliver a safe package but when you have a road full of AI driven perfection the result isn't quite what you expect. Consider the idea for a moment of an entire country's road network being filled with robot driven cars that have reached a density where to a reasonable approximation then entire network is one big interconnected road train. How can you estimate the effect of an accident in a remote location? Before you say that its easy consider the fact that a similar situation exists with the power grid and cascade failure still occurs. So - while it is nice that some simple models of simple cars produce some simple predictions that they are provably safe, should this be taken as a sign that the real world robot car is good to go? There are simply too many things left out of the model, and will be left out of any any future model, to be that confident. More information:Carnegie Mellon Methods Keep Bugs Out Of Software For Self-Driving Cars Adaptive Cruise Control:
If you would like to be informed about new articles on I Programmer you can either follow us on Twitter or Facebook or you can subscribe to our weekly newsletter. |
| Last Updated ( Thursday, 30 March 2017 ) |