| Deep Learning Chess |
| Written by Alex Armstrong | |||
| Wednesday, 17 December 2014 | |||
|
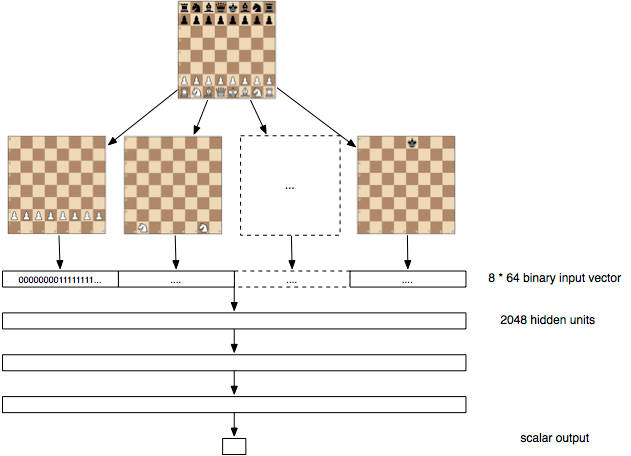
Usually chess playing programs take a search approach to finding good moves, but why not see if a deep neural network can do the job without the need to hand tune game algorithms. This is an interesting piece of research, or a demonstration depending on how you think about it. Recently deep neural networks have been impressing everyone by learning to recognize things. This raises the question of how good they are at learning things based on logic and strategy - the game of chess, say. This is the question that Erick Bernhardsson decided to tackle - mostly just for the fun of it. You don't have to know the theory of artifical neural networks to appreciate what is going on. Essentially a neural network can be used to learn a function from data. The key difference between the neural network and say a lookup table for the function is that you hope that the neural network will learn a model for the function that generalizes so that it gets close to the right answer for data that it hasn't seen. Usually the problem is that there is insufficient data to train the network but in this case the solution was to download 100 million games from the FICS Games Database. The neural network was 3 layers deep with 2048 neurons per layer. The input layer consists of a set of 12 blocks of 64 bit inputs. Each 64-bit block takes the positions for one of the 12 possible pieces on a bitmapped board. This is a reasonably good sparse distributed representation of the state of play and cleverly designed to give the neural network a chance of learning the sort of features that might be effective.
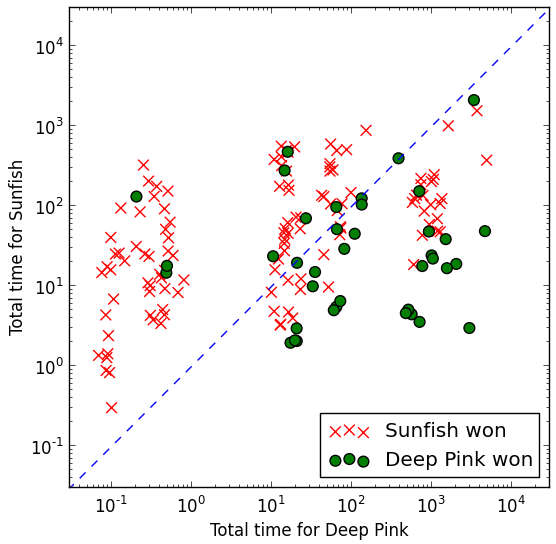
The assumption is that the data contains information about the evaluation function f(p) which gives you a measure of the goodness of a move,where p is 1 for an eventual win, 0 for an eventual draw and -1 for an eventual lose. You can assume that in an ideal game then each player will play optimal moves and hence: f(p)=-f(q) if move q, made by the other player follows q; and f(r)>f(q) where r is a random move rather than q because a random move must be better for the opponent than for the player choosing a better perhaps optimal move. These rules aren't perfect but they represent the behavior you would like the evaluation function to have. The network was trained by presenting it with triples (p,q,r), i.e. the current position, the move selected by the human player and a random move. The objective function, i.e. the function that measures the error of the network, was designed to make smaller errors correspond to the properties of the ideal evaluation function. There are some surprising things to note. First no model of chess, chess playing or the rules of chess are incorporated into the model. Second is that the objective function is simply allowing the network to optimize the theoretical properties of the evaluation function and there is again no sense of "win" or "lose" built into the model - indeed the model has no idea of the outcome of any of the triples applied. This means that it is learning without any idea of who wins given the data. Previous neural network chess playing programs, e.g. Sebastian Thrun's NeuroChess, have used the final outcome of the game to learn the evaluation function. So does it learn chess? The remarkable answer seems to be yes. The evaluation function learned can be put into any of the existing chess engines and hence it can be tested against hand crafted evaluation functions. The engine using the learned evaluation function was named Deep Pink in honour of IBM's Deep Blue. It was pitted against Sunfish - a chess engine written in Python - which isn't a highly rated chess engine but plays a reasonable game. You can make any evaluation function better by allowing the engine to search deeper, so what matters is how the two functions do against each other according to time. You can see the result in the diagram below.
Overall it is surprising that the network learned an evaluation function that works at all, but winning about 1/3 of the time is reasonably impressive. Erik has clearly a lot of work to do and he is working alone using an AWS GPU instance. The program is up on GitHub and there is a list of suggested improvements. I'd add to the list an investigation of the features that the network learns.
More cartoon fun at xkcd a webcomic of romance,sarcasm, math, and language More InformationLearning to Play the Game of Chess Related ArticlesNeural Networks Describe What They See Neural Turing Machines Learn Their Algorithms Synaptic - Advanced Neural Nets In JavaScript Google's Neural Networks See Even Better The Flaw Lurking In Every Deep Neural Net Google's Deep Learning AI Knows Where You Live And Can Crack CAPTCHA
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Wednesday, 17 December 2014 ) |