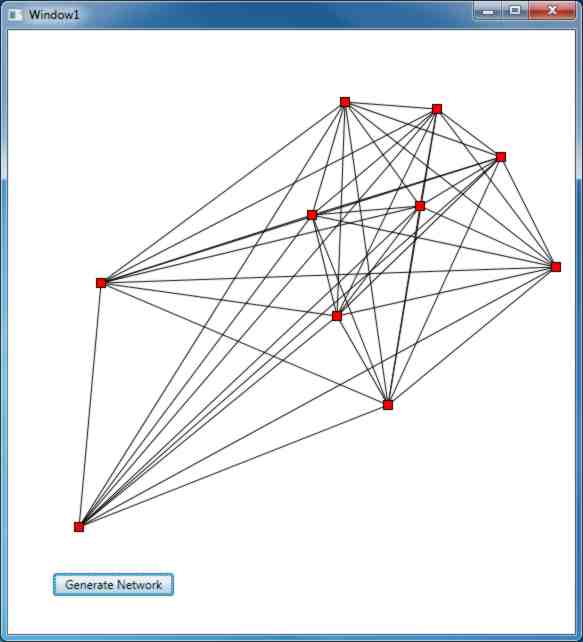
Prim's Algorithm In C# - The Network

Starting with a new C# WPF project we need to add a button labelled "Generate Network" and a Canvas object named canvas1. A Canvas object is often a good thing to use when you need to draw using x,y co-ordinates but there are other ways of doing the same job.

Moving to the code. We need an array to hold the co-ordinates of the points:

private Point[] Positions = new Point[size];

size is a constant that sets the size of the network in number of vertices.

const int size = 10;

The array to hold the network data can be defined as

private Single[,] Network = new Single[size, size];

We are also going to need a random number generator throughout the program so creating a global object is a good idea:

private Random R = new Random();

We can now write a method that fills both Position and Network with random values:

private void setnet(Single[,] Net,Point[] Pos)
{
 int maxlength = (int)(Math.Min(canvas1.Width,
                          canvas1.Height) * 0.9);
 int minlength = maxlength / size;
 for (int i = 0; i < size; i++)
 {
  Pos[i].X = R.Next(minlength, maxlength);
  Pos[i].Y = R.Next(minlength, maxlength);
  for (int j = 0; j <= i; j++)
  {
   Net[i, j] = distance(Pos[i], Pos[j]);
   Net[j, i] = Net[i, j];
   if (i == j) Net[i, j] = 0;
  }
 }
}

The points are generated randomly with co-ordinates between minlength and maxlength which are derived from the size of the Canvas object.

Notice that the distance array is made to be symmetric and the diagonal is also set to zero. The distance between points is computed using an additional function.

The distance function is simply the usual Euclidean formula:

private Single distance(Point a, Point b)
{
 return (Single)Math.Sqrt((a.X - b.X)*(a.X - b.X) +
                       (a.Y - b.Y) * (a.Y - b.Y));
}

Recall that C# has no power operator and simply multiplying things together is better than having to use the Maths object to square a value.

After generating the network it would be nice to view it. A drawing routine is quite easy – as long as you don't worry too much about efficiency. We can simply use Line objects to draw lines on the Canvas.

First we clear the Canvas of any child nodes it may already contain:

private void shownet(Single[,] Net)
{
 canvas1.Children.Clear();

Next we create a new Line object for each pair of points that have a non-zero distance between them:

Line myLine;
for (int i = 0; i < size; i++)
{
 for (int j = 0; j < i; j++)
 {
  if (Net[i, j] != 0)
  {
   myLine = new Line();
   myLine.Stroke = Brushes.Black;
   myLine.X1 = Positions[i].X;
   myLine.X2 = Positions[j].X;
   myLine.Y1 = Positions[i].Y;
   myLine.Y2 = Positions[j].Y;
   myLine.StrokeThickness = 1;
   canvas1.Children.Add(myLine);
  }
 }
}

Next we can plot suitable marker shapes at the position of each node:

 Rectangle myMarker;
 for (int i = 0; i < size; i++)
 {
  myMarker = new Rectangle();
  myMarker.Stroke =Brushes.Black;
  myMarker.Fill = Brushes.Red;
  myMarker.Height = 10;
  myMarker.Width = 10;
  myMarker.SetValue(Canvas.TopProperty,
      Positions[i].Y - myMarker.Height / 2);
  myMarker.SetValue(Canvas.LeftProperty,
      Positions[i].X - myMarker.Width / 2);
  canvas1.Children.Add(myMarker);
 }
}

Notice the way the that the position of the rectangle is set using an attached property on the Canvas object. This is a feature of WPF that beginners often find difficult. Attached properties are a good idea from the implementation point of view but they often don't help with readability and clarity. You might also ask why the Line object sets its own position without the need for an attached property and yet most of the other WFP shapes can't.

To try these out place a button on the form, if you already haven't and enter the following as the button's click routine:

private void Button_Click(object sender,

          RoutedEventArgs e)
        {         
            canvas1.Width = 600;
            canvas1.Height = 600;
            setnet(Network, Positions);
            shownet(Network);
        }

You can now try the program out and see if it really does generate reasonable graphs. It should! You can size the canvas control to make best use of the space and the graph will adjust itself to fill it, more or less. It is fun just to see the range of graphs that can be produced.

A typical random graph with ten vertices