John Conway's Life isn't just a fascinating program, it's an example of a cellular automaton. The theory of cellular automata (CA) sounds intimidating, but in fact it's simple and fun. It is a deep mystery how complex things arise from simple things – almost without even seeming to try. And how best to implement it? 

You can quote countless examples from almost any area of science. For example, classical mechanics describes the motion of particles using a very simple equation and yet this rapidly generates complex chaotic motions in fluids.

Similarly the laws of chemistry are simple and yet life seems to spontaneously generate itself from these simple rules. Even the genetic code is simple compared to the complex systems that result from its application.

For a long time the problem of how complexity arises from simplicity has puzzled and fascinated people. Perhaps here really does lie the secret of life.

One attempt to understand how simplicity controls the universe is to be found in the theory of cellular automata, CA. This sounds intimidating but its simple and fun. 

Although this article focuses on one particular type of  CA - Conway's Life - it is worth spending some time explaining what a general CA is. If you want more detail then see: Cellular Automata - The How and Why

The basic idea of a CA is that a large number of units – cells – are given a simple set of rules to follow. Notice that each cell obeys its rules without any global overview of what is happening. In this sense a CA is another embodiment of the principle

“Think global, act local”

and indeed what we are interested in is the global effect that such local rules have.

The origins of CAs are difficult to pin down but back in the early 1950s Stanislaw Ulam a mathematician at Los Alamos used the first digital computers to play with patterns that evolved with time. He called them “recursively defined geometry”.

The first true CAs were probably invented by Ulam’s close friend the well-known mathematician and computer scientist John Von Neumann. Ulam suggested that Von Neumann try to construct rule-based machines in an artificial universe that would help model self reproduction. He chose a chessboard universe in which each square represents a cell that can obey a set of rules.

This was the first cellular automaton.

The Rules Of Life

So far all of this sounds very abstract and perhaps the time is overdue for a real example – Life. This was devised in 1970 by John Horton Conway, a Cambridge mathematician, and made a public appearance via Martin Gardner’s column in Scientific American (Oct 1970 and Feb 1971). He was trying to simplify Von Neumann's self replicating machines. 

The rules of Life are very simple.

The universe is a rectangular grid with each grid square representing a cell, which can be either alive or dead (on or off if you want a less emotive description).

Each cell clearly has eight neighbor and what happens at each generation depends on how many neighbors N it has:

Next generation

2

No change

Alive or On

0,1,4-8

Dead or off

Notice that the rule is very simple.

If you imagine that you are a cell sitting in the middle of a huge rectangle of other cells it is very easy for you to find out what to do. You simply count how many of your eight neighbors are alive and if the result is 3 you set your state to “on” (irrespective of what it is currently). If it is exactly 2 then you don’t change your state and for any other value you set your state to Off.

If you want to be anthropomorphic about it you could say that a cell with fewer than two neighbors dies of loneliness, a cell with more than 3 neighbors dies of over crowding. and a cell with exactly three neighbors becomes alive (if it isn't already).

You can see that Life is an entirely local process in the sense that no cell has any idea of what it is going on globally. The question is can such a simple birth/death rule create anything that is interesting on a global scale?

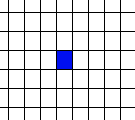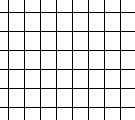
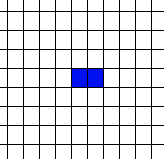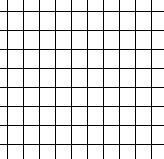
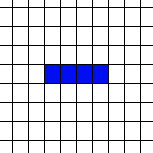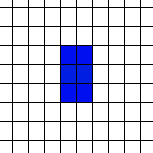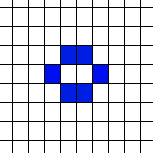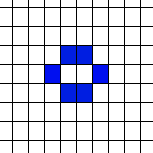
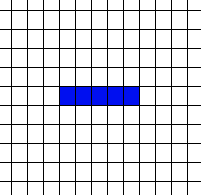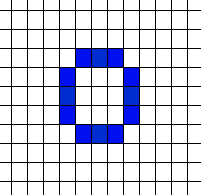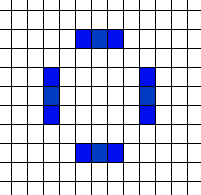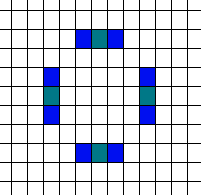
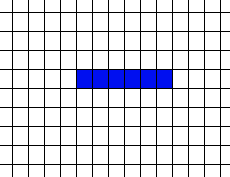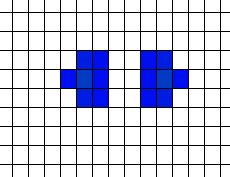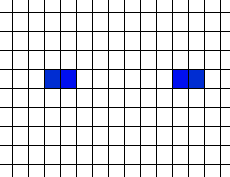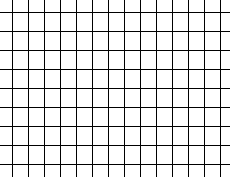
Life Is Complex

You might also think that Life, from the simplicity of the rule, is really going to be very boring and that large-scale structures are unlikely to happen – but in this case you would be wrong.

For example, just try and predict what will happen to a line of cells – one cell, then two, then three and so on.

1. A single cell dies at once.
   
   
   
   
2. Two cells also die at the first step
   
   
   
   however three cells do something remarkable and give the first hint that there is a lot going on here.
3. Three cells arranged in a horizontal line flip to three cells in a vertical line at the next generation and then back again to three in a horizontal row.
   
   
   
   We have an oscillator!
4. Four cells form a solid block and then a block with a hole in it that is stable and unchanging.
   
5. Five cells go through a sequence of changes to produce a set of four 3-cell oscillators.
   
   
6. Six cells go through a sequence of interesting shapes and then vanish.
   
   

So now attempt to use this sequence of behavior to make a law that explains or predicts the behavior of seven cells, eight cells or in general n cells. 

<ASIN:095511702X>

<ASIN:0195137183>

<ASIN:0262570866>