| What If Babbage..? |
| Written by Mike James | |||||
| Friday, 23 December 2022 | |||||
Page 1 of 4 What if the computer had been invented in the Victorian era? This isn’t a silly idea. Charles Babbage was born in the eighteenth century - the age of the Industrial Revolution. The calculating machines he invented, although never fully realized in his lifetime, are rightly seen as the forerunners of modern programmable computers. What if he had succeeded?
Charles Babbage
Charles Babbage had conceived of the basic principles of a stored digital computer in 1833 - and no I’m not talking of a glorified calculator. This was the real thing, CPU, memory and programs - and it could have been built using the technology of the time. If you visit the Science Museum in London you can see a working model of Babbage’s “Difference Engine”. It looks like a beautiful work of precision engineering and yet it was built using engineering tolerances that were available at the time. Babbage never built his difference engine, although others did build machines like it during his life time.
Working model of Babbage’s Difference Engine
Although the difference engine attracts most attention it isn’t a computer. It isn’t really even a straightforward calculator. It is specialised machine that will perform a particular type of calculation. One of the reasons Babbage didn’t complete his work on the difference engine is simply that he thought of something much better - the “Analytical Engine”. So why didn’t he build the analytical engine, was this really a step too far? One reason was that after people had funded the difference engine to no good result he wasn’t in a good position to raise funds for what looked like an even more risky bet. If he had raised the money then it seems fairly likely that the machine would have worked and the computer would have existed 100 years earlier than in reality. In 1910 his son, Henry P Babbage, built a large hand-operated calculator plus printer based on the CPU of the analytical engine - and it worked.
Working Analytical Engine
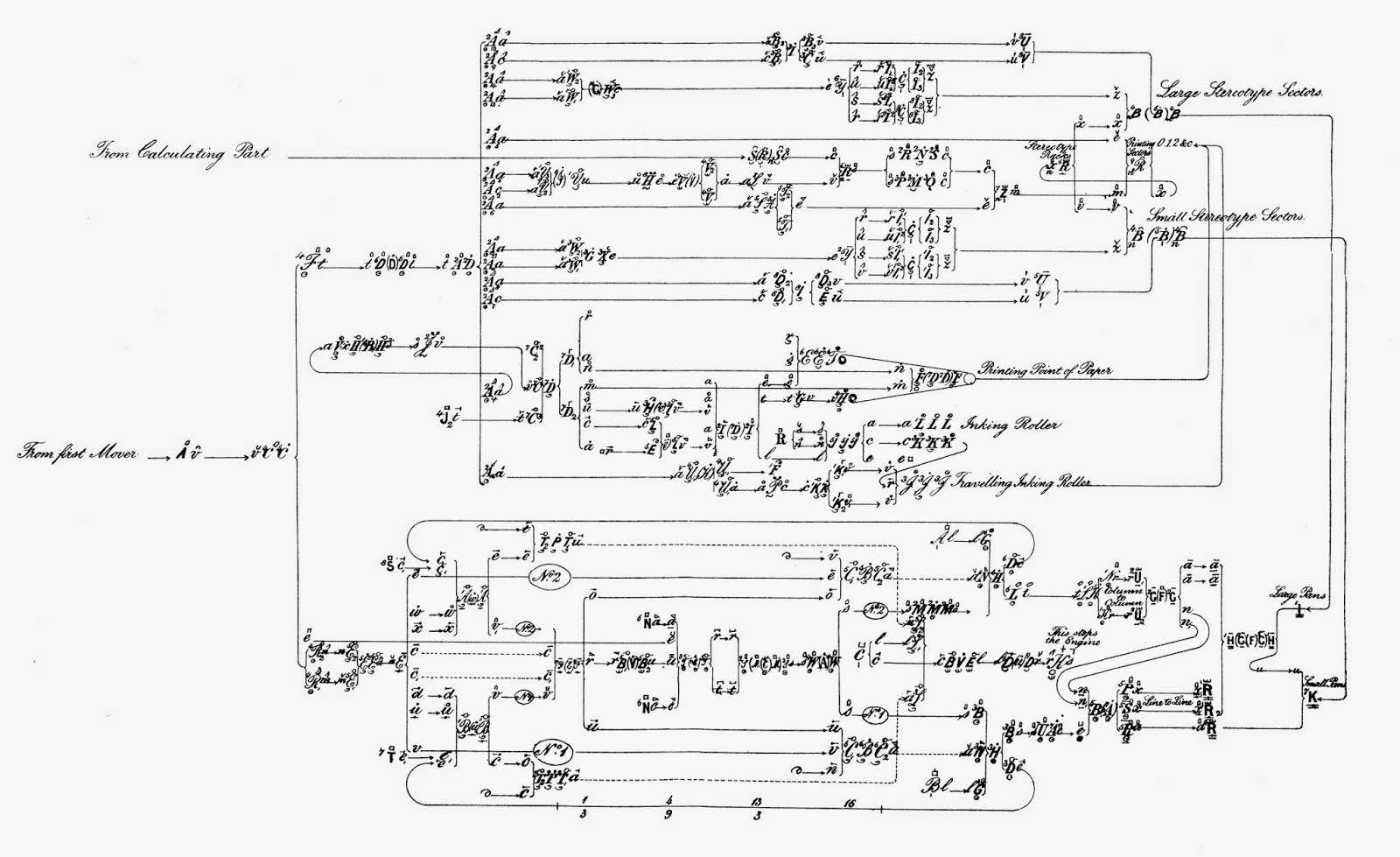
Now,170 years after Babbage drafted his original plans for the Analytical Engine, author, journalist and computer scientist John Graham-Cumming has an embarked on an ambitious, but realistic project to build one for public display. It is called Plan 28, a reference to the extensive documentation which Babbage left in a mahogany case that Babbage had constructed especially for the purpose. Graham-Cumming enlisted the help of Doron Swade, who, as curator of computing at the Science Museum in London, masterminded the building of the Difference Engine and as a preliminary step towards Plan 28 the the Science Museum has begun to digitise Babbage's entire archive of plans and notes. A Design Before Its Time?But surely even if Babbage had been successful it wouldn’t have changed anything? Babbage was so far ahead of his time that it would have just been a curiosity not a useful instrument? Not so. You would be surprised at just how sophisticated his ideas were. He had invented a notation for designing the calculating mechanisms - something like one of the chip design languages we use today - and he could have gone much further. He had plans for games arcades, chess playing machines, sound generators and desktop publishing - a Victorian computer revolution was entirely possible. Over the past few years we have reported on Plan 28, a new attempt, initiated by John Graham-Cumming in 2010, to reconstruct and formalize Babbage's design language. This research has made it clear that Babbage thought that it was his greatest invention and using it would allow even more sophisticated machines to be created. An example of the design language (Adrian Johnstone) More to the point with a working analytical engine other engineers and scientists would have understood what he was getting at. As it was, with only complex plans and his difficult to follow descriptions, very few grasped the fundamental idea of a computer. Imagine what the effect would have been had the idea of a computing engine spread like the idea of a steam engine. To quote Adrian Johnstone, Professor of Computing at Royal Holloway, University of London: "The notation, or more correctly Babbage's parallel notations showing the geometry, the timing, the causal chains and the abstract components of his machines, have a direct parallel in the Hardware Description Languages developed to aid the design of modern large scale integrated circuits. These languages typically have a geometry facet in which the arrangement of components in space is specified; a register transfer facet which emphasises the interconnection of functional units via registers and memory buses; and a behavioural facet which describes sequences as state machines or in software-like notations." Babbage even assumed that his design language would be taught in schools so that students could construct even more sophisticated and complex machines - of course this never happened. <ASIN:0142001449> <ASIN:0486246914> |
|||||
| Last Updated ( Friday, 23 December 2022 ) |