| Data Structures - Trees |
| Written by Mike James | ||||
| Sunday, 20 July 2025 | ||||
Page 2 of 3
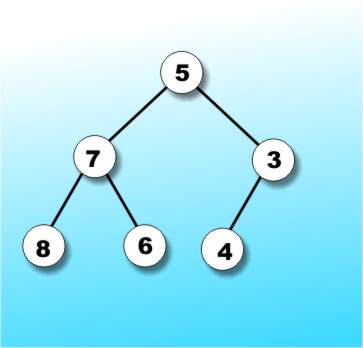
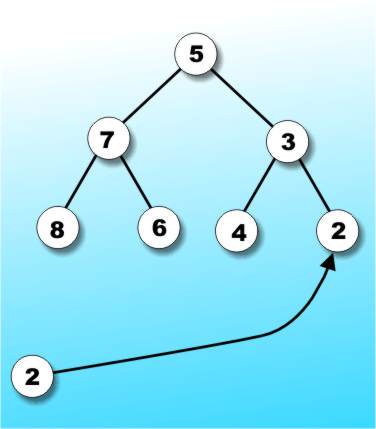
For example, if you already have the perfectly balanced tree in Figure 4a and the value 2 has to be added to it then the result is the perfectly balanced tree in Figure 4b.
Figure 4a: A perfectly balanced tree
Figure 4b: Adding (2) keeps the tree in balance.
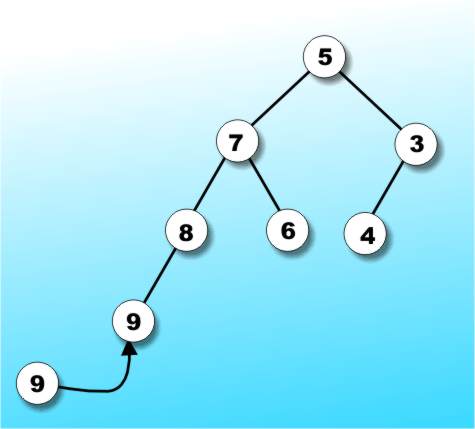
However it isn't always possible to insert a new data value and keep the tree in perfect balance. For example, there is no way to add 9 to the tree in Figure 4a and keep it in perfect balance (Figure 4c) without reordering chunks of the tree. It turns out the effort expended in reorganising the tree to maintain perfect balance just isn't worth it.
Figure 4c: Adding (9) makes the tree unbalanced
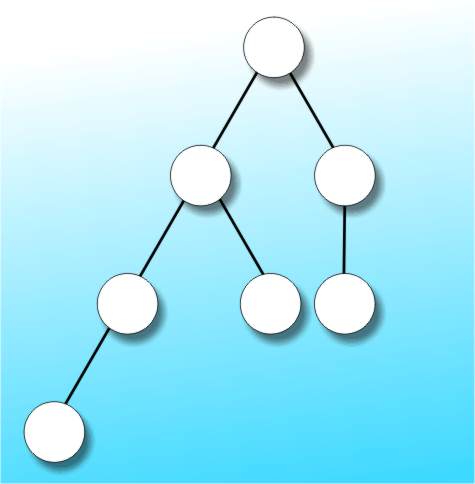
AVL TreesSo it looks as though using trees to store data such that searching is efficient is problematic. Well there might be a remedy if a less restricted form of balance were used. One such approach is to insist that the depths of each sub-tree differ by at most one. A tree that conforms to this definition is called an AVL tree, or sometimes just a "balanced" as opposed to "perfectly balanced" tree. Many programmers have puzzled what AVL might stand for - Averagely Very Long tree? The answer is that AVL trees were invented by Adelson-Velskii and Landis in 1962. Notice that every perfectly balanced tree is an AVL tree but the reverse isn't true as shown in Figure 5.
Figure 5: An AVL tree that isn't perfectly balanced
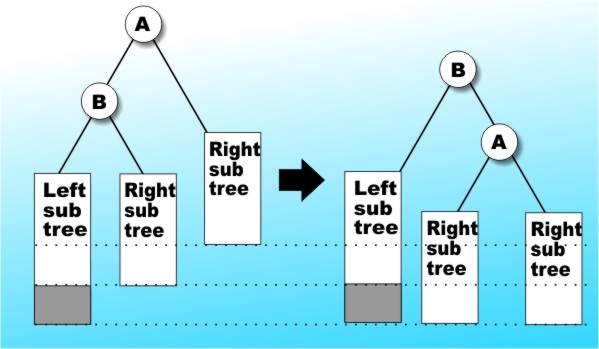
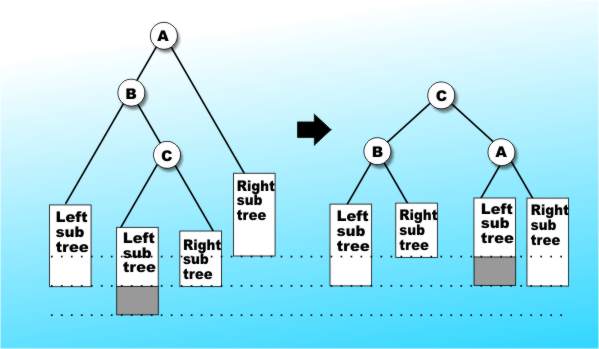
It turns out that an AVL tree will never be more than 45% deeper than the equivalent perfectly balanced tree. This means that searching an AVL tree is likely to be as quick as searching the tree in perfect balance and the payoff is that adding a node to an existing AVL tree so that it stays an AVL tree isn't difficult. In short re-balancing an AVL is easy, as can be seen in Figure 6a & b.
Figure 6a: A simple reorganisation converts a not quite AVL tree into an AVL tree
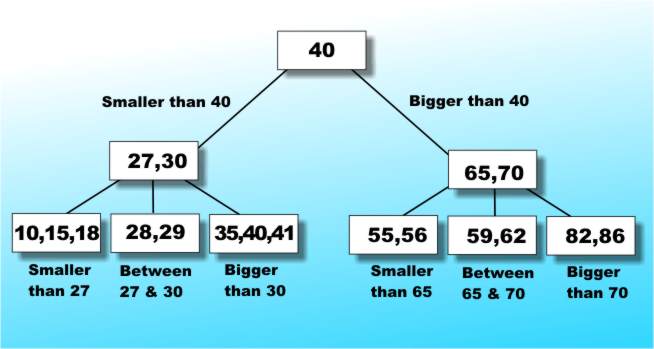
Figure 6b: A slightly more complicated example of a reorganisation converting a not quite AVL tree into an AVL tree B-TreesAt this point the story could come to an end and we could all happily use AVL trees to store data that needs to be found again in double quick time. Unfortunately AVL trees and binary trees in general aren't ideal when it comes to implementing an index stored on disk. The trouble is that disks are accessed one large chunk - i.e. a sector - at a time and mapping a search tree onto a disk so that there is one node per sector would produce a very slow search. One of the nicest ideas to get around this problem is the B-Tree. A B-Tree is constructed using a `page' of storage at every node. The B-Tree is constrained to have no fewer than n items and no more than 2n items on every page. In other words, the page size is fixed at 2n and we insist that at least 50% of the page is used if possible. The organisation of each page, and its links to the next page, is more complicated than for a binary tree but not that difficult. The m items on each page are entered in order and either a page is terminal or it has m+1 pointers to pages at the next level. The first pointer is to a page that contains items that are smaller than the first item on the page, the second is to a page that contains items that lie between the first and second item and so on to the last pointer, which points to pages that contain items larger than the last item. It sounds confusing but the example of a B-Tree in Figure 7 should make everything look simpler and make it possible to understand an exact definition of a B-Tree. A B-Tree of order n satisfies the following:
You can spend a few happy hours working out how this rather abstract definition results in the friendly B-Tree in Figure 7.
Figure 7: A B-Tree
You should also find it easy to work out the algorithm for searching a B-Tree. Basically it comes down to starting at the root page and if the key isn't found moving to the page that contains items in the same range as the one you are looking for. If there isn't a suitable descendant page then the item you are looking for isn't in the B-Tree and so you very likely have to add it. Notice that the number of page accesses required to find or not find an item is very reasonable.
<ASIN:0130224189> <ASIN:0817647600> <ASIN:0071353453> <ASIN:1852339772> |
||||
| Last Updated ( Sunday, 20 July 2025 ) |