Net from gross

Now to the question of undoing the effect of increasing or decreasing a quantity by a percentage.

If you know the Gross price including tax or other percentage charges and want to know the Net price without it, how do you work it out?

An attractive, but incorrect, line of reasoning is to say that as the Net price (i.e. without tax)  was increased by V% to give the Gross price (i.e. with tax) then the Gross price should be decreased by V% to get back to Net.

So a common but incorrect guess is that  Net=Gross*(1-V).

This is misguided because the amount add to Net, i.e. Net*V, isn’t the same as the amount subtracted from Gross i.e. Gross*V.

In general if you increase something by I% and then decrease the result by I% you do not get back to where you started!

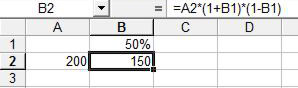
Increasing 200 by 50% and then decreasing it by 50% gets you back to 150

If you would like a demonstration that this method is incorrect then create the small spreadsheet shown above.

The value entered into A2 is increased by the percentage in B1 and then decreased by the same percentage. You can see in the figure that in the case of 200 and 50% the result is 150 which is very clearly not 200!

If you experiment with this spreadsheet what you will find is that for small values and small percentages the difference between the original value and the calculated value can be quite small and this sometimes leads people to believe that the answer is in fact correct except for a small arithmetic error.

This is of course not true but on occasion the approximation can be useful if you are working things out in your head.

The correct answer depends on a simple rearrangement of the formula:

Gross=Net*(1+V)

to give the Net in terms of the Gross:

Net=Gross/(1+V)

That is, if you multiply by (1+V) to get the Gross you have to divide by (1+V) to get back to the Net.

In general:

• if you know that a value has been increased by I% and you want to calculate the original value divide by (1+I)
  
  
• if you know that a value has been decreased by I% and you want to calculate the original value divide by (1-I)

Adding percentages

Percentages don’t always work in exactly the way that you might think.

The example in the previous section of the erroneous calculation of Net from Gross price should have put you on your guard.

For another example consider the following question - is taking P% of something and then Q% of the result the same as taking P%+Q% of the original value?

Putting this in more practical terms if you are offered a discount of 10% on a price and then offered a further discount of 5% is this the same as a 15% discount?

First let's consider taking successive percentages of something.

Taking P% and then Q% of a value is just:

=value*P*Q

and this is quite clearly not the same as:

=value*(P+Q)

To see that this is the case just try a few examples using a spreadsheet and you will quickly discover that the results that the two formulas produce are very different.

For example, if you take 10% of 100, i.e. 10, and then take 20% of this the result is 2, but (10+20)% i.e. 30% of 100 is 30.

In other words, if you take successive percentages of something they don’t add they multiply. Taking 10% followed by taking 20% of the result is the same as taking 2% of the original (i.e.0.1*0.2).

When reasoning or bargaining with percentages it is usual to speak of “another 1%” in the sense of increasing the percentage offered by adding one percent. In this case it does look as if percentages add but notice that in this particular case all the percentages refer to a proportion of the same whole. That is you are being offered an increase of 1% in the percentage not an additional 1% of what you already have.

In general best way to think about ways of combining percentages is by considering slices of a pie. If you are negotiating for an additional percentage of the whole pie then certainly percentages add but if you are arguing for a percentage of the slice you have already been allocated then they multiply.

Although mathematically the difference is very obvious it is often lost in the detail of negotiation - on purpose.

A 10% gain and a 10% loss

So in many cases you can be misled by adding percentages.

This is also true if you increase or decrease a value by P% and then Q%.  In general

• Increasing or decreasing a quantity by P% and then Q% is not the same as increasing or decreasing it by (P+Q)%

Consider the 10% discount followed by an additional 5% discount.

In this case the first discount makes the price:

=value*(1-P)

and the second takes it to:

=value*(1-P)*(1-Q)

which is clearly not the same as a discount of P+Q percent which would be:

=value*(1 - (P+Q))

Multiplying out the brackets in the first expression gives:

=value*(1 - (P+Q)+P*Q)

Comparing the two results indicates that a P% discount followed by an additional Q percent discount gives an overall discount that is smaller by P*Q than a P+Q discount.  

The same rule works for percentage increases and a P percent increase followed by a Q percent increase actually gives you an increase of P+Q+P*Q i.e. a bigger percentage increase than P+Q by P*Q. 

So a 10% discount followed up by a 5% discount only gives you an overall discount of 14.5% and not the 15% you might expect.

The point here is that it matters whether you are being offered a (10+5)%, i.e. 15% discount, or a 10% discount followed by a further 5%. 

This gives us the answer to the discount on a discount problem posed earlier.

Unless you know if the sales person intended to give you a total discount of 15% or alternatively a further discount on the discounted price the actual price you will have to pay isn’t clear.

In most cases an additional discount is usually meant in the literal sense of adding to the initial discount - i.e. the intended discount is 10%+5% and not 5% more off the discounted price - what is important is that you realise that there are two possible interpretations.

As another example of how percentages do not add up in the way that you might suppose consider the following simple problem.

A trader makes a 10% profit on an investment in the first part of the day but before the day is out has made a 10% loss - is the total profit zero?

The commonsense answer to this question is that the 10% gain is wiped out by the 10% loss, but this reasoning does not take into account the fact that the percentages are calculated on different values.

Suppose the initial investment was $100, then a 10% gain is $10 and this makes the total investment worth $110. The following 10% loss reduces the investment by $110*0.1 or $11, making the final investment worth only $99. Hence a 10% gain followed by a 10% loss does not take you back to square one.

Also notice that it does not matter in which order the loss or gain occurred. The answer is exactly the same, a 1% loss on the initial value.

Of course, if both the percentages were quoted relative to the initial investment then the percentages would add up because 10% of $100 is always $10. Again, what is important here is that you realise that there are two possible meanings and you should always discover what value a percentage change is using as its starting point.