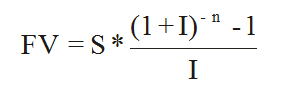| Present and Future Values |
| Written by Janet Swift | |||||||||||||||||||
Page 5 of 6
A regular cashflowNow that we have a definition of both the NPV and NFV it it time to use them to look at some situations that we have already analysed in earlier chapters. In particular what is the NPV or NFV of a perfectly regular cashflow as might be found as part of a repayment loan, annuity or savings plan. If you receive $S at the end of each period for n periods the NPV is given by:
which should remind you of the calculation to find the future value of a cashflow. In that case the sum was the same but each value of S was multiplied by (1+I) raised to a power. By comparing the two expressions it isn’t difficult to work out that:
and comparing this to the formulas given in Chapter 4 also reveals that:
In other words the NPV of a regular cashflow is just its present value as calculated in Chapter 4. This is very reasonable as the present value of a cashflow is simply what it would be fair to pay if you were purchasing an annuity. Put another way, it is the amount you need to invest now to generate the cashflow at I% per annum. If you regard the cashflow as the repayments of a loan then the present value is equal to the amount of the loan. Again this is perfectly reasonable. In the case of a savings plan the reasoning is slightly different because there is no sum of money changing hands now - only the cashflow being invested. However there is a well defined future value - the final value of the investment. In this case the present value is the amount that you would have to invest now to produce the same future value as the cashflow. For example,if you invest $1000 per annum at 10% (effective) for 10 years the future value is:
and the present value is
If you invest $6144.56 at 10% for 10 years you will receive:
So investing $1000 per year for 10 years is the same as a making a one-off investment of approximately $6,144. Again the concept and terminology of ‘present value’ of a cashflow makes perfect sense. You can choose to look at either the present value or the future value of a cashflow. In each case the future value is what the cashflow is finally worth and the present value is what it is worth now allowing for interest at I%. No matter what the source or the purpose of the cashflow is the present value is calculated using:
or the corresponding FV function. In each case the PV and FV are equal to the NPV and NFV and they are related in by the standard formula
or
For simplicity we are assuming that all cashflows are at the end of each time period. This idea of present and future values of a cashflow has a pleasing symmetry but the interpretation of PV and FV is different in each of the standard situations of a repayment loan, annuity and savings plan. These are summarised in the table below. If we assume that a transaction generates a series of equal cash payments then the present and future values can be interpreted as follows:
You can see that in the case of a repayment loan and the annuity the present value is more meaningful than the future value and in the case of the savings plan both are meaningful. |

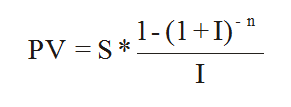 or the corresponding PV function and the future value is calculated using:
or the corresponding PV function and the future value is calculated using: