| Pre-History of Computing |
| Written by Historian | |||
Page 1 of 2
When was the dawn of computing? We tend to date it from the middle of the 20th century when the first programmable computers were built in the UK, the USA and also in Russia and Germany. Prior to that "computers" referred to people who performed calculations - and in this article we look at the history of making calculations. An age old problemIf you have few numbers to add up - no problem. Even if you want to calculate the orbitals of the hydrogen atom you can do it, as long as you know how. In this day and age arithmetic is never a problem, unless you have massive computational designs. Yet only a short time ago even simple sums taxed the human brain to the extent that the growth of commerce and government was severely limited by the difficulty of adding 2 and 2. Today we think of all the things that computers can do for us and we know why we want one - keeping in touch with our Facebook friends; Internet banking; downloading MP3s, playing the latest blockbuster game - and oh yes, just occasionally we crunch some numbers. But in the early days doing sums was the main reason for wanting or inventing the computer. You could say that the need to add two and two and make four was the driving force behind computing. Limitations of notationBefore you can even begin to think of automating arithmetic you have to have a good basic system to automate. From our smug standpoint this seems ridiculously easy, but just try adding CXVII to LXIIV to see what I mean. The chances are that the Romans would have had a better grasp of the pure sciences, and Roman engineering would really be something to marvel at, if only they had a simpler notation for arithmetic! More seriously the problems of running the empire, collecting taxes and such like would have been more possible. The Romans weren't the only ones to have problems with their notation. The Greeks and the Chinese were similarly handicapped. Hence the old story that the Greeks would rather argue philosophically about the number of teeth that a horse had rather than go over and count them - given their numeric notation arguing was probably easier and more certain! From hieroglyphics to caclulating machinesTo give you some idea just how complex a notation can be consider the ancient Egyptian system - 1 to 9 were represented by vertical lines, 10 by U, 100 by a coiled rope, 1,000 a lotus blossom, 10,000 a pointed finger, 100,000 a tadpole, and 1,000,000 was expressed by a man with arms stretched toward heaven in amazement. So to write 3,647,543 you would have to show: 3 amazed men Don't ask how you would perform multiplication using this notation! AbacusPerhaps because of the difficulties of their particular notation, the Chinese and the Japanese were the first to invent a mechanical aid to calculation. During the first half of this century the Chinese and Japanese abacus in the hands of a skilled operator could beat even the best western mechanical calculator.
An abacus Thankfully eventually things settled down and the Hindu-Arabic 0 to 9 place value notation was adopted worldwide. This made arithmetic, especially multiplication and division, so much easier that it became practical. It still wasn't so easy that anyone could do it and through the ages the ability to do arithmetic was the skill of the mathematician. Even educated people knew very little of how numbers worked. Samuel Pepys for example complained of having to stay up late swotting his eight times table. Business men and accountants struggled to learn tables beyond the usual 12 times 12 - up to 24 times 24, for example. Logs and BonesJohn Napier, a Scottish mathematician, took it on himself to make arithmetic easier for the masses. He fancied himself as an inventor and set about the task in this spirit.
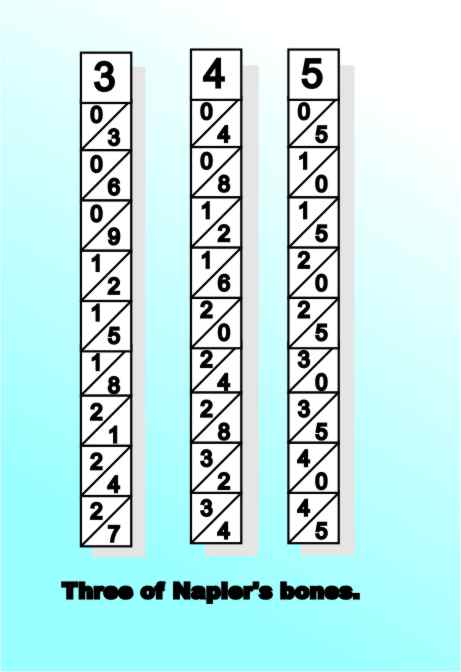
John Napier (1550-1617) Napier is best known for the idea of using logarithms in 1614 to make arithmetic easier - but he didn't invent the closely related slide rule. Every number has a logarithm and adding logarithms is the same a multiplying the original values. If you have two numbers that you want to multiply you look up their logs, add the logs together and then look up the antilog. Of course dividing is just a matter of subtraction. Logs make multiplication and division easy - but only if you have suitable tables in which to look up the logs and anti-logs. It was the need to compute such tables that started Charles Babbage off thinking about his difference machine and eventually to formulate his conception of the modern computer. As well as logarithms, Napier's name is forever coupled with Bones. Napier's Bones (1617) were a set of rods with multiplication tables written out on them. Users could select rods for a particular multiplication and then, by adding up the partial products, get a final answer. As well as coping with multiplication a rod was included for square and cube roots. Napier's Bones
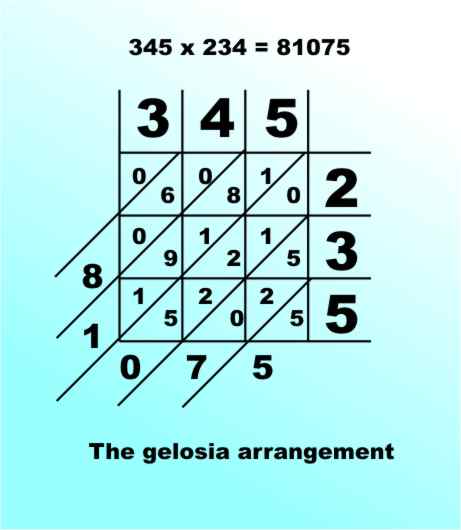
Napier's Bones were based on a method of multiplication known much earlier by the name Gelosia. You write the two products along the sides of a grid and write out the results in the body of the grid. As each pair of digits can produce a two digit number any "tens" part is written in the top diagonal and the "units" part in the bottom. Finally adding along the diagonals gives the final answer:
Napier's Bones were multiplication tables written out in the Gelosia form. You selected the bones corresponding to the digits of the first value and read of the partial products corresponding to the second value - adding these up along the diagonals gives the final result:
The fact that the Bones were important is more a measure of how poor the population were at arithmetic rather than how clever or sophisticated the Bones were. One thing they were very certainly not was the forerunner of the slide rule. <ASIN:1116149044> <ASIN:1402757964> <ASIN:0486270963> <ASIN:0471375683> <ASIN:039304002X> <ASIN:0395745195>
|
|||
| Last Updated ( Thursday, 03 April 2025 ) |