| Donald Knuth's Christmas Tree Lecture 2017 |
| Written by Mike James | |||
| Wednesday, 13 December 2017 | |||
|
This year's Donald Knuth annual Christmas lecture is on a brand new problem that doesn't have a long history and this is the point. He shows that math is a lively and exciting subject. The video is well worth seeing. It is a well established Stanford University tradition that in December Donald Knuth puts on a flamboyant jumper and delivers a public lecture that, if at all possible, features a tree structure of some sort or another. This year seems to be another tree-free year so I suppose it should be a non-xmas tree lecture. It is called "A Conjecture That Had To Be True", but its real value is that it give you some idea of what math research is all about. The blurb for the event reads: A few months ago, the speaker did some extensive calculations relating to a curious problem in combinatorial geometry; and the resulting numbers satisfied an amazing formula. Although this formula was known to be true only in the five or six smallest cases of the problem, it was impossible to imagine a decent world in which the formula would not hold universally. Come to the lecture and learn about the interesting sequel.
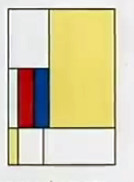
The problem is very simple and starts from a division of a rectangle into other smaller rectangles - a Mondrian problem? For example:
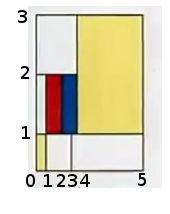
You can characterize the division by assigning integers to each of division lines. So the example above becomes:
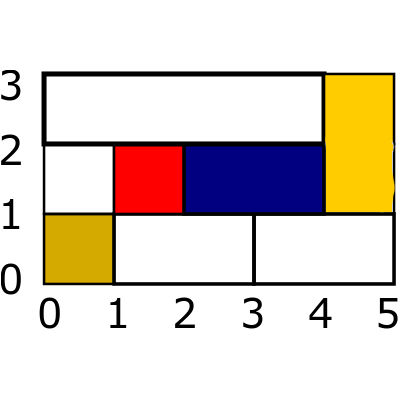
The next step is to form a reduced configuration which essentially means drawing out the coordinates of the dividing lines with equal sized squares:
This is what Knuth refers to as a reduced pattern and you can see that the rectangles have the same co-ordinates. You can also see that this is equivalent to the original mondrian pattern. Whenever you get a combinatorial arrangement like this the question is always "how many. possibilities are there?". In this case the question of interest is "how many tight pavings are there?". A tight paving is a reduced paving with the minimum number of rectangles. It turns out that for an n x m arrangement the smallest number of rectangles in a reduced arrangement is n+m-1. So a tight paving is one that uses n+m-1 rectangles - but how many of these are there for any n x m? Knuth gives examples in the video for 2 x 2, 3 x 2 so that you can understand the idea. Of course as the size goes up you have to use a computer and this is what produced the conjecture about the relationship between n, m and the number of tight pavings. Now watch the video - it is a tour de force of mathematics as it happens. If you know who Donald Knuth is skip to 1:45 to avoid the introduction.
There are so many interesting things in this video but it is the slow progress from the concrete to the abstract that is so interesting and it illustrates how mathematical thinking works very nicely.
More InformationDonald Knuth's Annual Christmas Lecture Related ArticlesKnuth's 22nd 360 Degree Not Christmas Tree Lecture Knuth's 21st Not Christmas Tree Lecture The Art Of Computer Programming The Ace Gift For Any Programmer Donald Knuth's Christmas Tree Lecture Donald Knuth and the Art of Programming Another Chunk of The Art of Computer Programming
To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Thursday, 14 December 2017 ) |