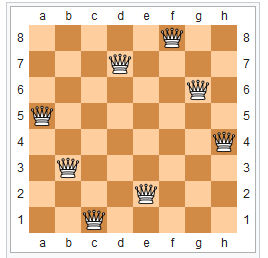
Well not really - but it is still an interesting move in the right direction to understand this most simple of configuration problems.

The eight queens problem is well known and of major use as an example of recursively solving a problem. It was first proposed in 1848 in a German chess magazine, but I first encountered it in an elegant account by Dijkstra in his Notes On Structured Programming. It was used as an example of how recursion-based backtracking can be used to solve a problem far more easily than any other approach. I can't say I've thought about it much since, apart from using it as an advanced example of recursion.

For eight queens on a standard 8 x 8 chess board there are 92 possible solutions, but there are only 12 fundamental solutions - the others are derived from symmetry. There is also only one symmetric solution, as shown below:

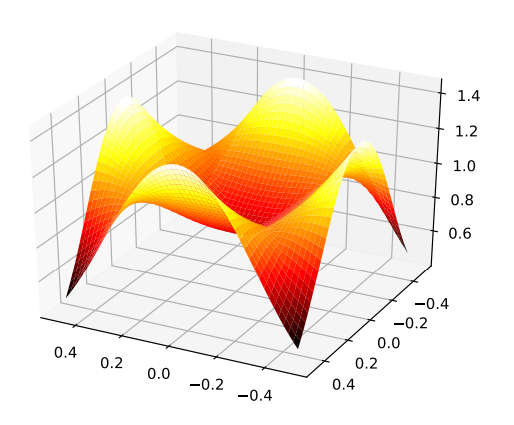
A more interesting problem is the generalization to n queens placed on an n x n board. Finding how many configurations there are for general n was recently proved to be NP-hard and so any solution, even approximations, are interesting. We know the exact numbers for n < 28. Beyond this our computers cannot take us - for now.

The latest news is that Michael Simkin, a postdoctoral fellow at Harvard's Center of Mathematical Sciences and Applications, has the result that there are about (0.143n)ⁿ different arrangements of n queens on an n x n board.

Mathematician Answers Chess Problem About Attacking Queens

Quanta Magazine

This is being headlined as a "solution", but of course the detail is in the use of the word "about". This result is not an upper or lower bound, but an approximate order as n gets bigger. The approximation makes use of the fact that not all squares on a finite board are of equal value in placing the queen. The square in the middle makes more positions unavailable to another queen than a square on the edge. What this means is that solutions tend to use edge squares rather than central squares. The distribution of queens in a solution can be visualized as:

The techniques developed in the arXiv paper might well lead on to more results (Q(n) is the number of ways of placing n queens on an n x n board):

"This paper combined the entropy method and a randomized algorithm to determine the first and second order terms of log(Q(n)). We wonder whether similar methods might succeed in obtaining more accurate estimates. More generally, for many classes of combinatorial designs (such as Steiner systems and high-dimensional permutations), denoting by X(n) the number of order-n objects, the first and second order terms of log(X(n)) have been determined using similar methods. It would be very interesting to improve these estimates."

• Mike James is the author of The Programmer’s Guide To Theory which sets out to present the fundamental ideas of computer science in an informal and yet informative way and devotes a chapter to a discussion of what makes a problem NP-hard.

More Information

THE NUMBER OF n-QUEENS CONFIGURATIONS 
by Michael Simkin

Related Articles

N Queens Completion Is NP Complete

Rubik's Cube Is Hard - NP Hard

Column Subset Selection Is NP-complete

Unshuffling A Square Is NP-Complete

NP-Complete - Why So Hard?

NP Complete

Classic Nintendo Games Are NP Hard

Physics Is NP Hard

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info