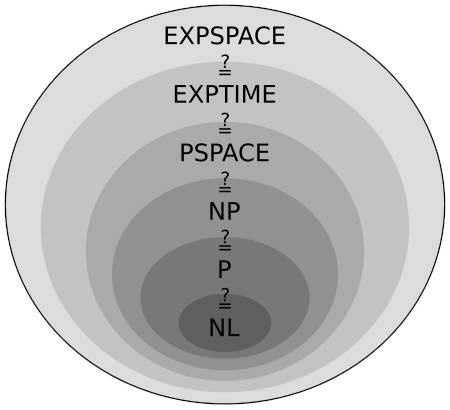
You may well know that important conjecture that P! = NP, but of equal theoretical importance is P! = PSPACE, but it hardly gets any of the publicity of its near relation. We seemed to have moved a little closer to proving it.

We are all fairly familiar with the idea of the complexity class P which are the problems we can solve in polynomial time. Perhaps a better way to express P is the class of problems that have solutions that scale in time like a polynomial in the size of the problem.

What we often overlook is the idea of the class PSPACE. At the same rough level of exactitude, PSPACE is the class of problems that scale in space like a polynomial. In this context. "space" means the amount of storage used. The time part of the classification is simply the time a Turing machine takes to solve a problem of size n and space is the amount of the tape used in solving the problem. There are some technical things we can do to make the idea clearer - for example you really don't want to include the data needed to express the problem, so we usually consider a multi-tape Turing machine which has a program tape that cannot be written to and a data tape which is read/write. 

We all know that we can usually trade time for space. If you want a program to complete faster then throw memory at it. If you are working in limited memory then the algorithm usually takes longer. This raises the more exact question of how time and space are related in computation. The two classes P and PTIME seem to be related in some way, but are they equal? That is, if a problem can be solved in polynomial time does that imply that it can be solved using polynomial memory and vice versa?

One importance of the P and PSPACE question is that if P = PSPACE, i.e. if all polynomial time-solvable problems are solvable in polynomial space and vice versa then P = NP. However, as most believe that P!= NP, it seems likely, if not as intuitive, that P!= PSPACE.

After a bit of logical manipulation, you can come to the conclusion that to prove that P! = PSPACE all you need to do is find a problem that can be solved in O(n) SPACE that cannot be solved in O(n^k) time for all k>1. The recent breakthrough is that problems that can be solved in O(n) SPACE need at least O(n^2-e) in time. This doesn't prove that P!= PSPACE as it is an example where SPACE is better then time O(n) compared to at worst O(n²).

You can characterize this as space is worth more than time, but I like to think that it reveals how far we have to go to find an example of an algorithm that scales like O(n) in time but something like O(n²) in space.

• Mike James is the author of The Programmer’s Guide To Theory which sets out to present the fundamental ideas of computer science in an informal, and yet informative, way. Another of his books, The Trick Of The Mind: Programming and Computational Thought, aimed at programmers and non-programmers alike, examines the nature of programming and reveals why it is a very special skill

More Information

Simulating Time With Square-Root Space

For Algorithms, a Little Memory Outweighs a Lot of Time

Related Articles

A Computable Universe - Roger Penrose On Nature As Computation    

NP-Complete - Why So Hard?       

How Much Math Is Knowable?

Classic Nintendo Games Are NP Hard       

Physics Is NP Hard       

Pancake flipping is hard - NP hard       

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info

<ASIN:B081YS81L7>

<ASIN:B09MDL5J1S>