| Cannibal Animal Games |
| Written by Mike James | |||
| Sunday, 30 June 2013 | |||
|
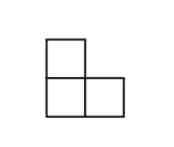
If you are looking for a new 2D game to implement on a mobile device, then you might like to know about Cannibal Animals. It also has its serious side in that it reveals something about 2D geometry and its complexity. The game of Cannibal Animals was invented a year ago or more, but there are some new theoretical results concerning it. It is a simple game played on a 2D grid and at its heart it's a variant of Tic-Tac-Toe and derived from a similar class of games presented by Harary. The game is played on an infinite grid of squares. Each opponent takes a turn to occupy squares. Player A can only occupy a single free square and their goal is to construct a particular shape - an animal. The animal can be in any orientation and location and a reflected copy is also fine. Player B has to stop A from constructing an animal by placing an animal shape on the board. Notice that A only occupies one square per move but B occupies a set of squares. You can see that the game is in the same general area as Tic-Tac-Toe in that one player is trying to occupy a particular set of squares and the other is trying to stop them. For example if the animal is the L-shaped triomino:
Then a game might evolve along the following five plays:
First A plays black square 1 and B responds with the L labeled 1. Then A responds with black square 2 and B places a triomino 2 on th board. Finally A plays black square 3 and wins. A few minutes of experimentation should convince you that there is no way for B to win by stopping A from creating a triomino. An animal that provides B with a winning strategy is called a cannibal and one that provides A with a winning strategy is called a non-cannibal. The idea is that B's animal either eats A's or not. And the first, obvious result is that any animal with three or fewer cells is a non-cannibal. However pushing this result to animals with four cells is still a conjecture and no counter examples. The latest provides a proof that various regular shapes are cannibals. There are also plenty of open questions concerning the game and quite a few theorems listed in the paper. However, it is worth mentioning the theorem that for n>5 there exists both a cannibal and a non-cannibal animal. This might be useful in extending the game. If you are into theoretical computer science why not see if you can prove any of the outstanding problems - e.g. prove that all five celled animals are non-cannibals. If you are into AI, what about an AI approach to playing the game? On the other hand you could simply find a way to make the game more compelling as a mobile phone app.
More InformationCannibal Animal Games: a new variant of Tic-Tac-Toe Jean Cardinal, Sébastien Collette, Hiro Ito, Matias Korman, Stefan Langerman, Hikaru Sakaidani, Perouz Taslakian Related ArticlesUnshuffling A Square Is NP-Complete The Revolution In Evolutionary Game Theory - Prisoners Dilemma Solved? Goldbach Conjecture - Closer to Solved? The Physical Travelling Salesman Challenge Classic Nintendo Games Are NP Hard
To be informed about new articles on I Programmer, install the I Programmer Toolbar, subscribe to the RSS feed, follow us on, Twitter, Facebook, Google+ or Linkedin, or sign up for our weekly newsletter.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Sunday, 30 June 2013 ) |