| Modifiable encryption |
| Written by Alex Armstrong | |||
| Tuesday, 22 June 2010 | |||
|
You may soon be able to let your sensitive data free on the net to be processed by any number of cloud based servers and all secure in the knowledge that, while they can make changes to it, they never have access to it. The trick is called "homomorphic encryption" and it is the most exciting idea in cryptography for a decade.
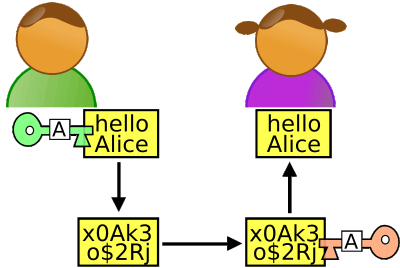
It may not sound exciting but "fully homomorphic encryption" is a much sought-after feature of an encryption system. The idea is fairly easy to explain. Suppose you have a value, an auction bid say, and it is encrypted to keep it away from the prying eyes of others. Now suppose that you need to add one to the current bid. At the moment the only way to do it is to take the encrypted value, decrypt it, add one and re-encrypt it. If you don't know how to decrypt the value then there is no way you can modify it. Unfortunately this means that if you want something or someone to make a change to your encrypted data you have no choice but to give them complete access to it.
However fully homomorphic encryption makes it possible for a user to change an encrypted value without knowing what it is or how to decrypt it. That is, if you have an operation that you want to perform on the plain text, a fully homomorphic encryption system will allow you to perform an operation, usually not the same operation, on the ciphertext which when the ciphertext is decrypted gives the same result. It's a bit like being able to manipulate the contents of a sealed envelope without opening it or knowing what it contains. If such a system existed it isn't difficult to think up uses for it - a secure voting procedure for example. It is also obvious that such an encryption scheme is particularly important in this age of cloud computing. Fully homomorphic encryption would allow cloud services to both store and manipulate your data without ever knowing what it contained or having access to it. At the moment there are a number of partially homomorphic encryption systems which support a single operation, either addition or multiplication. A fully homomorphic system supports addition and multiplication and hence all arithmetic operations. In 2009 a fully homomorphic encryption system was invented by Craig Gentry (thesis: A Fully homomorphic Encryption Scheme). He started from a "somewhat homomorphic encryption" scheme which sounds like a very imprecise and unmathematical term. The idea is that you can create systems that are homomorphic but as you add and multiply cyphertexts they accumulate "noise" that eventually makes them undecipherable. Gentry took a somewhat homomorphic system and demonstrated how to improve the coding to remove the noise, so producing a fully homomorphic system. Unfortunately Gentry's system is too complex to implement for realistic levels of security.
Symetric encryption both Bob and Alice have to have the same key to the data (Odder) Since Gentry's discovery other people have been working towards a more practical system and things have been edging their way towards a fully implementable system that can be used for a range of new applications. At the end of 2009 Marten van Dijk, Craig Gentry, Shai Halevi and Vinod Vaikuntanathan presented a simplified fully homomorphic system: Fully Homomorphic Encryption over the Integers. Even more recently N.P. Smart and F. Vercauteren published another simpler scheme Fully Homomorphic Encryption with Relatively Small Key and Ciphertext Sizes. Both results use the conversion of a "somewhat" homomorphic encryption scheme into a fully homomorphic scheme by using cleaning to correct the accumulating noise. So far it seems that to make cleaning effective very large parameter sizes are needed and it is this that makes the whole scheme inefficient. Given the number of times the algorithm will be applied in any real application efficiency really is important. You can think of it as having to build in an error correcting code into the cipher. Each valid ciphertext has to be surrounded by a unique bubble of invalid ciphertexts that the manipulation, addition and multiplication, transforms the ciphertext into. These invalid ciphertexts cannot be decoded but as each one is uniquely associated with a valid ciphertext the "cleaning" process can correct the code by replacing it with the closest valid ciphertext. The actual cleaning method works by using a second key to recrypt the data and remove the errors. It seems likely that a practical homomorphic system will be created very soon and in recognition of his work on June 16th 2010 Craig Gentry was awarded the Doctoral Dissertation award from the ACM worth $20,000. Gentry's path into mathematics and a problem of some importance to computing is also an interesting one. He first graduated from Harvard Law School, but with a bachelor's degree in math as he was bored with intellectual-property law. In 2005 Gentry enrolled in Stanford's Ph.D. program, and in June 2008 took a three-month internship with IBM where he invented the algorithm that is causing all the fuss. Update: 19 April 2011Gentry was given the 2010 ACM Grace Hopper award for his work on homomorphic encryption and the US military research agency, DARPA, has awarded research contractor Galois Inc almost $5 million to speed the performance of his algorithm. See: DARPA spends $20 million on homomorphic encryption
<ASIN:0387779930> <ASIN:3540492437> <ASIN:0883857197> <ASIN:0471597562> <ASIN:1584885513> <ASIN:0201616475> undecipherable |
|||
| Last Updated ( Saturday, 28 May 2016 ) |