Error correcting codes are essential to computing and all sorts of communications. At first they seem a bit like magic. How can you possibly not only detect an error but correct it as well? How do they work? In fact it turns out to be very easy to understand the deeper principles.

This is an extract from my recent book on theory:

A Programmers Guide To Theory

Now available as a paperback and ebook from Amazon.

Contents

1. What Is Computer Science?
   Part I What Is Computable?
2. What Is Computation?
3. The Halting Problem
4. Finite State Machines
   Extract 1: Finite State Machines
5. Practical Grammar
6. Numbers, Infinity and Computation
   Extract 1: Numbers 
   Extract 2: Aleph Zero The First Transfinite
   Extract 3: In Search Of Aleph-One
   Extract 4: Transcendental Numbers
   
7. Kolmogorov Complexity and Randomness
   Extract 1:Kolmogorov Complexity 
8. The Algorithm of Choice
9. Gödel’s Incompleteness Theorem ***NEW!
10. Lambda Calculus
    Part II Bits, Codes and Logic
11. Information Theory 
12. Splitting the Bit 
13. Error Correction 
14. Boolean Logic
    Part III Computational Complexity
15. How Hard Can It Be?
    Extract 1: Where Do The Big Os Come From
16. Recursion
    Extract 1: What Is Recursion
    Extract 2: Why Recursion
17. NP Versus P Algorithms
    Extract 1: NP & Co-NP
    Extract 2: NP Complete

<ASIN:1871962439>

<ASIN:1871962587>

Error correcting codes are essential to computing and communications. At first they seem a bit like magic - how can you possibly not only detect an error but correct it as well? In fact, it turns out to be very easy to understand the deeper principles.

The detection and correction of errors is a fundamental application of coding theory. Without modern error correcting codes the audio CD would never have worked. It would have had so many clicks, pops and missing bits due to the inevitable errors in reading the disc, that you just wouldn't have been able to listen to it. Photos sent back from space craft wouldn't be viable without error correcting codes. Servers often make use of ECC memory modules where ECC stands for Error Correcting Code and secure data storage wouldn't be secure without the use of ECC. Finally the much-loved QR Code has four possible levels of error correction with the highest level allowing up to 30% of the code to be damaged: 

This QR code can still be read - its a link to Wikipedia - due to error correcting Reed Solomon codes.

So how does error detection and correction work?

Parity Error

There is a classic programmer's joke that you have probably already heard:

Programmer buys parrot. Parrot sits on programmer’s shoulder and says “pieces of nine, pieces of nine,..”. When asked why it isn’t saying the traditional “pieces of eight” the programmer replies, “It’s a parroty error!”

Parity error checking was the first error detection code and it is still used today. It has the advantage of being simple to understand and simple to implement. It can also be extended to more advanced error detection and correction codes.

To understand how parity checking works consider a seven-bit item of data:

0010010

If this was stored in some insecure way, then if a single bit was changed from a 0 to a 1 or vice versa you would never know. If, however, instead of storing eight bits, we store nine, with the ninth – the parity bit – set to make the total number of ones odd or even, you can see that a single-bit change is detectable.

If you select odd parity then the eight bits are:

1 0010010

i.e. the parity bit is a 1, and if any of the bits changes then the parity changes from odd to even and you know there has been a bit error.

Parity checking detects an error in a single bit but misses any errors that flip two bits, because after any even number of bit changes the parity is still the same.

This type of error checking is used when there is a fairly small probability of one bit being changed and hence an even smaller probability of two bits being changed.

Hamming Distance

When you first meet parity error detection it all seems very simple, but it seems like a “one-off” rather than a general principle. How, for example, do you extend it to detect a two-bit or three-bit error? In fact, parity checking is the simplest case of a very general principle but you have to think about it all in a slightly different way to see this.

When a bit is changed at random by noise you can think of the data word as being moved a small distance away from its true location. A one-bit change moves it a tiny amount, a two-bit change moves it further and so on. The more bits that are changed the further away the data word is from its original true location. A simple measure of this distance between two data words is to count the number of bits that they differ by. For example, the two data words 011 and 110 are two units apart because they differ in two places – the first and last bits. This is called the Hamming distance after R. W. Hamming who did much of the early work into error detection and correction.

Richard Hamming 1915-1998

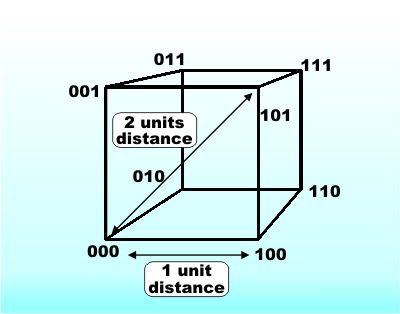
What has Hamming distance got to do with parity checking? Simple - if you take a valid data word which has a parity bit associated with it and change a single bit then you have a data word which is one Hamming unit of distance away from the original. Every valid code word has an invalid code word one unit away from it.

To imagine this it is easier to think of a three-bit code. In this case you can draw a cube to represent the location of each possible code word.

A code cube

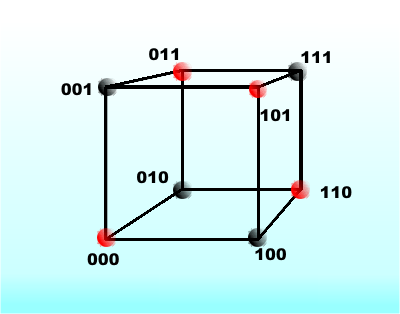
If we treat all even parity words as valid and odd parity words as invalid, you can see at once that a code such as 000 is surrounded by invalid codes one unit away, e.g. 001, 010 and 100. If you move two units away then you reach valid codes again. What is more, every valid code is surrounded by a cluster of invalid codes one unit away. In other words, a single-bit error always moves a valid code to an invalid code and hence we detect the error.

Red corners are valid codes – black invalid

<ASIN:1569756287>

<ASIN:1579124852>